Упершому будинку 36 квартир, а в другому 50. у другому булинку поверхів на 2 менше. а квартир на кожному поверсі на 2 більше. знайти кількість поверхів у кожному будинку та кількість квартир на кожному поверсі

Скорость грузового - 40, легкового - 50

за первый час легковой догонит грузового на 50-40=10 км

за второй на 10+(55-40)=25 км. и тд. каждый час все больше.

Положим, что первый член равен 10, тогда второй - 15 ,третий 20 и т.д.

Сумма членов прогрессии 10,15,20,25... должна равнятся 135

Сумма АП равна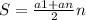 , но т.к. последний член не известен выразим an через a1 и n: 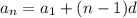и формулу суммы можно переписать в виде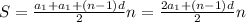

Подставим известные данные

Решим квадратное уравнение

Положительный корень x = 6 показывает количество членов Ап. т.е. часов за которые легковой догонит грузового

1.

s=153
s1=10m/c*t
s2=(3+(3+5*(t-1))*t\2 -это ареф прогресия где коичество членов будет определятся временемt

уровнение:
10*t+(3+(3+5*(t-1))*t\2-153=0
20t+t+5t^2=306
решая кв.ур находим 
t1=6
t2<0 - не уд условию.
отв:t1=6

2.Обозначим скорости поездов x и y, а расстояние от A до станции s. 
То, что они прибыли на станцию одновременно дает уравнение: 
s / x = (60–s) / y 
То, что ни прибудут на станцию одновременно при увеличении скоростей – еще одно: 
s / (x+25) = (60–s) / (y+20) 
а то, что это случиться на 2 часа раньше – третье: 
s / x = s / (x+25) + 2 

Осталось решить эту систему, причем, поскольку находить s не требуется, можно сразу вычислить его из третьего уравнения s = 2·x^2 / 25 + 1 и подставить в первые два, получится система уравнений с двумя неизвестными, 
решая которую получим 
ответ: x = 12.5·( √33 / 3 – 1), y = 10·(√33 / 3 – 1)