Объяснение:
Выделим в левой части полный квадрат. Для этого прибавим к обеим частям уравнения выражение и перенесем слагаемое в левую часть:
1)
Тогда примет вид
Левая часть неотрицательна. Правая часть, учитывая рассматриваемый интервал, строго отрицательна. Значит, корней на данном интервале нет.
2)
Возможны 2 случая:
2.1)
Оба корня принадлежат рассматриваемому интервалу, а значит являются корнями исходного уравнения.
2.2)
То есть корень не принадлежит рассматриваемому интервалу.
4
а)ОДЗ:
{ tan(x) ≥0 (Т.к. подкоренное выражение всегда неотрицательно)
{ cos(x) ≠0 (Т.к. тангенс это синус, делённый на косинус,а на ноль делить нельзя)
Произведение равно нулю,когда хотя бы один из множителей равен нулю
1) 2sin²(x)-3cos(x) = 0
Из основного тригонометрического тождества sin²(x)+cos²(x) = 1 выразим синус
sin²(x) = 1-cos²(x)
2(1-cos²(x))-3cos(x) = 0
2-2cos²(x)-3cos(x) = 0|:(-1)
2cos²(x)+3cos(x)-2 = 0
Пусть cos(x) = t, -1 ≤ t ≤ 1, тогда
2t²+3t-2 = 0
D = 3²-4*2*(-2) = 9+16 = 25 = 5²
Второй корень меньше -1,поэтому мы его рассматривать не будем
Вернёмся к замене
Если t = 0,5, тогда
cos(x) = 0,5
Это равенство распадается на совокупность двух:
[ x = arccos(0,5) + 2пn, n∈Z
[ x = -arccos(0,5) + 2пn, n∈Z
[ x = п/3 + 2пn, n∈Z
[ x = -п/3 + 2пn, n∈Z
Второй корень не подходит по ОДЗ,так что единственное решение этого равенства x = п/3 + 2пn, n∈Z
Дробь равна нулю,когда числитель равен нулю,а знаменатель не равен нулю
{ sin(x) = 0
{ cos(x) ≠ 0
{ х = пn, n∈Z
{ x ≠ п/2 + пn, n∈Z
Пересечений с ОДЗ нет,поэтому наше решение входит в ответ
б) Находим количество решений на отрезке [0;2П] ( см. вложение)
По рисунку мы видим,что у уравнения на данном отрезке 4 корня(0,п/3,п,2п)
Объяснение:
Выделим в левой части полный квадрат. Для этого прибавим к обеим частям уравнения выражение и перенесем слагаемое
и перенесем слагаемое  в левую часть:
в левую часть:
1)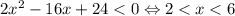
Тогда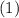 примет вид
примет вид
Левая часть неотрицательна. Правая часть, учитывая рассматриваемый интервал, строго отрицательна. Значит, корней на данном интервале нет.
2)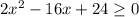
Возможны 2 случая:
2.1)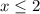
Тогда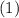 примет вид
примет вид
Оба корня принадлежат рассматриваемому интервалу, а значит являются корнями исходного уравнения.
2.2)
Тогда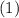 примет вид
примет вид
То есть корень не принадлежит рассматриваемому интервалу.
4
Объяснение:
а)ОДЗ:
{ tan(x) ≥0 (Т.к. подкоренное выражение всегда неотрицательно)
{ cos(x) ≠0 (Т.к. тангенс это синус, делённый на косинус,а на ноль делить нельзя)
Произведение равно нулю,когда хотя бы один из множителей равен нулю
1) 2sin²(x)-3cos(x) = 0
Из основного тригонометрического тождества sin²(x)+cos²(x) = 1 выразим синус
sin²(x) = 1-cos²(x)
2(1-cos²(x))-3cos(x) = 0
2-2cos²(x)-3cos(x) = 0|:(-1)
2cos²(x)+3cos(x)-2 = 0
Пусть cos(x) = t, -1 ≤ t ≤ 1, тогда
2t²+3t-2 = 0
D = 3²-4*2*(-2) = 9+16 = 25 = 5²
Второй корень меньше -1,поэтому мы его рассматривать не будем
Вернёмся к замене
Если t = 0,5, тогда
cos(x) = 0,5
Это равенство распадается на совокупность двух:
[ x = arccos(0,5) + 2пn, n∈Z
[ x = -arccos(0,5) + 2пn, n∈Z
[ x = п/3 + 2пn, n∈Z
[ x = -п/3 + 2пn, n∈Z
Второй корень не подходит по ОДЗ,так что единственное решение этого равенства x = п/3 + 2пn, n∈Z
2)
Дробь равна нулю,когда числитель равен нулю,а знаменатель не равен нулю
{ sin(x) = 0
{ cos(x) ≠ 0
{ х = пn, n∈Z
{ x ≠ п/2 + пn, n∈Z
Пересечений с ОДЗ нет,поэтому наше решение входит в ответ
б) Находим количество решений на отрезке [0;2П] ( см. вложение)
По рисунку мы видим,что у уравнения на данном отрезке 4 корня(0,п/3,п,2п)