Алгебра: Упрости выражение sin 66 + sin^2 26 + sin 28 + cos ^2 26

Упрости выражение
sin 66 + sin^2 26 + sin 28 + cos ^2 26

Показать ответ

Ответ:

пппп103

07.01.2023 02:43

-3.

Объяснение:

√(6 -2√5) - √(9+4√5) =

Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:

6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =

(√5 -1)^2.

9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =

(√5 + 2)^2.

Именно поэтому решение запишется так:

√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l

Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:

(√5 - 1) - (√5 + 2) =

Упрощаем получившееся выражение:

√5 - 1 - √5 - 2 = -1 -2 = -3.

ответ: -3.

Использованные тождества:

а^2 - 2аb + b^2 = (a-b)^2;

а^2 + 2аb + b^2 = (a+b)^2;

√(a)^2 = lal.

0,0(0 оценок)

Ответ:

koteika282

17.11.2020 05:57

Так как при вращении на 360°=2П радиан , мы попадаем в ту же точку ,

то угол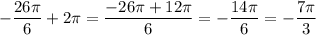 $-\dfrac{26\pi }{6}+2\pi =\dfrac{-26\pi +12\pi }{6}=-\dfrac{14\pi }{6}=-\dfrac{7\pi }{3}$ попадает в ту же

точку на единичной окружности , что и угол (-26П/6) .

Но угол (-7П/3) не лежит между 0 и 2П . Поэтому надо прибавить не 2П,

а больше , чтобы попасть в промежуток [ 0 ; 2П ] . Подбираем число n .

Если прибавить 3*2П , то получим

$-\dfrac{26\pi }{6}+3\cdot 2\pi =\dfrac{-26\pi +36\pi }{6}=\dfrac{10\pi }{6}=\dfrac{5\pi }{3}=300^\circ\ \ ,\ \ \ \ \dfrac{5\pi }{3}\in [\ 0\ ;\ 2\pi \ ]$

Полученный угол принадлежит промежутку [ 0; 2П ] .

Замечание. Если прибавить 2*2П , то не получим угол из

промежутка [ 0;2П ] . Действительно,

$-\dfrac{26\pi }{6}+2\cdot 2\pi =\dfrac{-26\pi +24\pi }{6}=\dfrac{-2\pi }{6}=-\dfrac{\pi }{3}$ .

То есть можно сообразить, что в числитель к (-26П) надо прибавить число, большее 26П, чтобы получить положительный угол. И соответственно подбирать n .

Если прибавить 4*2П , то получим угол, который больше, чем 2П. Действительно,

$-\dfrac{26\pi }{6}+4\cdot 2\pi =\dfrac{-26\pi +48\pi }{6}=\dfrac{22\pi }{6}=\dfrac{11\pi }{3}=660^\circ 360^\circ$