Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .
Рассмотрим многочлен , где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена :
- степень определяется выражением , то есть степень равна 84
- свободный член равен
- степень определяется выражением , то есть степень равна 6
Наконец, для многочлена получим:
- степень определяется выражением , то есть степень равна 90
Сумма степени и свободного члена многочлена :
ответ: 98
≈ 24,6°
Объяснение:
Для начала найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az}
AB = {3 - 3; -2 - (-1); 2 - (-3)}
AB = {0; -1; 5}
CD = {Dx - Cx; Dy - Cy; Dz - Cz}
CD = {1 - 2; 2 - (-2); 2 - 3}
CD = {-1; 4; -1}
Теперь найдем скалярное произведение векторов:
AB · CD = ABx · CDx + ABy · CDy + ABz · CDz
AB · CD = 0 · (-1) + (-1) · 4 + 5 · (-1)
AB · CD = 0 - 4 - 5
AB · CD = -9
Затем найдем длины векторов:
|AB| =
|CD| =
|CD| = 3
Найдем косинус угла между векторами:
cos =
cos = ≈ -0.41602514716892186
И наконец-то находим по таблице брадисса угол, с найденого косинуса
Это ≈ 24,6°
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение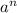 .
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение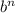 .
.
Рассмотрим многочлен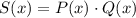 , где:
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена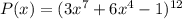 :
:
- степень определяется выражением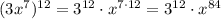 , то есть степень равна 84
, то есть степень равна 84
- свободный член равен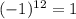
Для многочлена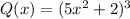 :
:
- степень определяется выражением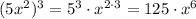 , то есть степень равна 6
, то есть степень равна 6
- свободный член равен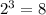
Наконец, для многочлена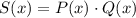 получим:
получим:
- степень определяется выражением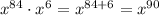 , то есть степень равна 90
, то есть степень равна 90
- свободный член равен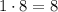
Сумма степени и свободного члена многочлена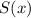 :
:
ответ: 98
≈ 24,6°
Объяснение:
Для начала найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az}
AB = {3 - 3; -2 - (-1); 2 - (-3)}
AB = {0; -1; 5}
CD = {Dx - Cx; Dy - Cy; Dz - Cz}
CD = {1 - 2; 2 - (-2); 2 - 3}
CD = {-1; 4; -1}
Теперь найдем скалярное произведение векторов:
AB · CD = ABx · CDx + ABy · CDy + ABz · CDz
AB · CD = 0 · (-1) + (-1) · 4 + 5 · (-1)
AB · CD = 0 - 4 - 5
AB · CD = -9
Затем найдем длины векторов:
|AB| =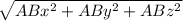
|AB| =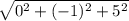
|AB| =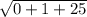
|AB| =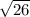
|CD| =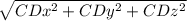
|CD| =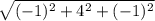
|CD| =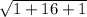
|CD| =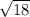
|CD| = 3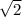
Найдем косинус угла между векторами:
cos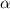 =
= 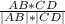
cos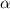 =
= 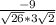
cos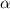 =
= 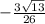
cos = ≈ -0.41602514716892186
= ≈ -0.41602514716892186
И наконец-то находим по таблице брадисса угол, с найденого косинуса
Это ≈ 24,6°