Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
Нидл
27.10.2021 09:04 •
Алгебра
Упростить выражение.
((cos2b-cos6b)/(sin6b-sin2b))+tg2b
Показать ответ
Ответ:
Zero00000
10.04.2022 20:30
решение смотри на фотографии
0,0
(0 оценок)
Ответ:
Миша3111
10.04.2022 20:30
Формулы:
,
,
.
0,0
(0 оценок)
Популярные вопросы: Алгебра
Nyashka12
29.12.2021 20:12
Найдите значение выражения....
Kira369
02.06.2021 22:13
Найдите коэффициенты квадратного уравнения...
Диана149018
10.01.2020 10:23
6×(3х-7) - 8(х-3) можно ответ?...
kholmatova002
14.03.2020 06:31
Найди значение выражения: (5а — 12b) - (5а + 12b) — 25а если а = 3 и b = 0,1....
таня2023
17.06.2022 09:22
. 11. Вычислите значение выражения...
Criss666
30.08.2020 18:44
Существует ли такое х, при котором у=-150...
Пепечка
30.08.2020 18:44
Разложите на множители ( _ значит дробь): 2_3x^3 - 8_27х 7y^5 - 7_4y^3...
hrustam2004
30.08.2020 18:44
3а = ? 2а-10 при каком значении переменной не имеет смысла выражения? а)0; б)10; в)5; н)0,5....
qwertyspro
30.08.2020 18:44
Решите систему уравнений: {5х-3у+8=0, {х+12у=11...
Алисик980
30.08.2020 18:44
2*(х-у)+х-у разложите на множители а+б*(а+2с)+2с...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
решение смотри на фотографии
Формулы: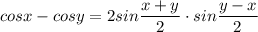 ,
,