По определению модуля.
Значит, при переходе через точку x=-2 выражения различаются.
Аналогично и остальные модули.
Таких точек в данном выражении четыре:
x=-2; x=8; x=-9; x=4,5
Эти точки разбивают числовую прямую на 5 промежутков.
Раскрываем модули на каждом промежутке:
1)
(-∞;-9]:
x+2 < 0 ⇒ |2+x|=-2-x
x-8 < 0 ⇒ |x-8|=-x+8
2x+18 < 0 ⇒ |2x+18|=-2x-18
Тогда
|2+x|-|x-8|+|2x+18|- = -2-x-(-x+8)+(-2x-18)-(-x+4,5)=-x-32,5
2)
(-9;-2]:
2x+18 > 0 ⇒ |2x+18|=2x+18
|2+x|-|x-8|+|2x+18|- = -2-x-(-x+8)+(2x+18)-(-x+4,5)=3x+3,5
3)
(-2;4,5]:
x+2 > 0 ⇒ |2+x|=2+x
|2+x|-|x-8|+|2x+18|- = 2+x-(-x+8)+(2x+18)-(-x+4,5)=5x+23,5
4)
(4,5; 8]:
|2+x|-|x-8|+|2x+18|- = 2+x-(-x+8)+(2x+18)-(x-4,5)=3x+16,5
5)
( 8;+ ∞]:
x-8 > 0 ⇒ |x-8|=x-8
|2+x|-|x-8|+|2x+18|- = 2+x-(x-8)+(2x+18)-(x-4,5)=x+32,5
О т в е т.
По определению модуля.
Значит, при переходе через точку x=-2 выражения различаются.
Аналогично и остальные модули.
Таких точек в данном выражении четыре:
x=-2; x=8; x=-9; x=4,5
Эти точки разбивают числовую прямую на 5 промежутков.
Раскрываем модули на каждом промежутке:
1)
(-∞;-9]:
x+2 < 0 ⇒ |2+x|=-2-x
x-8 < 0 ⇒ |x-8|=-x+8
2x+18 < 0 ⇒ |2x+18|=-2x-18
Тогда
|2+x|-|x-8|+|2x+18|-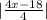 = -2-x-(-x+8)+(-2x-18)-(-x+4,5)=-x-32,5
= -2-x-(-x+8)+(-2x-18)-(-x+4,5)=-x-32,5
2)
(-9;-2]:
x+2 < 0 ⇒ |2+x|=-2-x
x-8 < 0 ⇒ |x-8|=-x+8
2x+18 > 0 ⇒ |2x+18|=2x+18
Тогда
|2+x|-|x-8|+|2x+18|-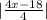 = -2-x-(-x+8)+(2x+18)-(-x+4,5)=3x+3,5
= -2-x-(-x+8)+(2x+18)-(-x+4,5)=3x+3,5
3)
(-2;4,5]:
x+2 > 0 ⇒ |2+x|=2+x
x-8 < 0 ⇒ |x-8|=-x+8
2x+18 > 0 ⇒ |2x+18|=2x+18
Тогда
|2+x|-|x-8|+|2x+18|-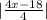 = 2+x-(-x+8)+(2x+18)-(-x+4,5)=5x+23,5
= 2+x-(-x+8)+(2x+18)-(-x+4,5)=5x+23,5
4)
(4,5; 8]:
x+2 > 0 ⇒ |2+x|=2+x
x-8 < 0 ⇒ |x-8|=-x+8
2x+18 > 0 ⇒ |2x+18|=2x+18
Тогда
|2+x|-|x-8|+|2x+18|-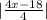 = 2+x-(-x+8)+(2x+18)-(x-4,5)=3x+16,5
= 2+x-(-x+8)+(2x+18)-(x-4,5)=3x+16,5
5)
( 8;+ ∞]:
x+2 > 0 ⇒ |2+x|=2+x
x-8 > 0 ⇒ |x-8|=x-8
2x+18 > 0 ⇒ |2x+18|=2x+18
Тогда
|2+x|-|x-8|+|2x+18|-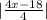 = 2+x-(x-8)+(2x+18)-(x-4,5)=x+32,5
= 2+x-(x-8)+(2x+18)-(x-4,5)=x+32,5
О т в е т.