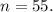Упростите выражение -0,14b + 0,18b -0,23b + 0,14b и найдите его значение , если а) b= -3,6
б) b= 6 2/3

Уровение:

(х+1)=2х

Х+1-2х=0

-х+1=0

-х=-1

Х=1

Задача 1

ПознаемУзнаем цена булочки, в случае если ведомо, собственно что пирожное на 18 руб. дороже, а цена 5 пирожных оформляет цена 11 булочек. Оформляем уравнение, где:

Х - цена булочки;

Х + 18 - цена пирожного.

Получаем:

11Х = 5 * (Х + 18);

11Х = 5Х + 90;

11Х - 5Х = 90;

6Х = 90;

Х = 90 / 6;

Х = 15 руб..

2) Познаем какую цена содержит пирожное, в случае если на 18 руб. дороже, чем булочка, а цена булочки составила 15 руб..

15 + 18 = 33 рубля.

ответ: стоимость пирожного 33 рубля, а булочка стоит 15 руб..

1) Аналитический.

2) Рекуррентній.

3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...

4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.

5)

6)

7) Это арифметическая прогрессия.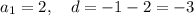

8)

ответ: нет, не является, потому что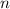 должно быть натуральным числом.

9)

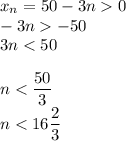
Наибольшее натуральное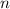 , удовлетворяющее этому неравенству, — это 16.

ответ: 16 членов.

10)

Второе решение не подходит, поскольку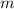 должно быть натуральным числом.

ответ: