1) Область определения - вся числовая прямая, это значит, что этот параметр не влияет на четность(функция может быть как четной, так и нечетной, так и общего вида)
2) Функция четна, если f(-x) = f(x), проверяем, f(-x) = 5 + 3x^3 и это не равно f(x), значит функция не может быть четной
3) Функция нечетна, если f(-x) = -f(x), проверяем, f(-x) = 5 + 3x^3 и это не равно -f(x), значит функция не может быть нечетной
4) Таким образом, эта функция ни четная ни нечетная, т.е. эта функция общего вида
Объяснение:
1) а) В уравнении один корень когда модуль равен 0, а он принимает это значение при а=-3
б) уравнение не имеет корней, когда модуль равен отрицательному числу, то есть число а лежит в интервале (-2;2)
2) х=-2/а
х=3/(а+2)
х=(а-3)/(а-3)=-1
3) a)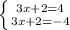
значит либо 3х=2, то есть х=2/3, либо 3х=-6, то есть х=-2
б) так как модуль больше нуля при любых х, то корней нет, так как он равен -2
в) x^2+x=0 ⇒ x(x+1)=0⇒ x1=0; x2=-1
г) 1.|x+3|-4=1 или |x+3|-4=-1
|x+3|=5 или |x+3|=3
х+3=5 или х+3=-5 или х+3 =3 или х+3=-3
х=2 или х=-8 или х=0 или х=-6
Ни четная ни нечетная(функция общего вида)
Объяснение:
1) Область определения - вся числовая прямая, это значит, что этот параметр не влияет на четность(функция может быть как четной, так и нечетной, так и общего вида)
2) Функция четна, если f(-x) = f(x), проверяем, f(-x) = 5 + 3x^3 и это не равно f(x), значит функция не может быть четной
3) Функция нечетна, если f(-x) = -f(x), проверяем, f(-x) = 5 + 3x^3 и это не равно -f(x), значит функция не может быть нечетной
4) Таким образом, эта функция ни четная ни нечетная, т.е. эта функция общего вида