Условие задания:
Дана функция y = f(x), где f(x) = 5/x. Найди f (2)
(ответ округли до сотых).
ответ: f(2)=

Показать ответ

Ответ:

ПаучьяХватка

09.12.2021 08:30

ОДЗ:

$\left \{ {{x^2+2x-20} \atop{ {x^2+2x-2\neq1 }\atop{\frac{|x+4|-|x|}{x-1}0 }} \right.$

Решаем каждое неравенство:

x^2+2x-20 ⇒ (x+1)^2-3 0 ⇒ $(x+1-\sqrt{3})(x+1+\sqrt{3})0$

$x\in (-\infty;-1-\sqrt{3}) \cup{-1+\sqrt{3};+\infty)$

$x^2+2x-2\neq 1$ ⇒ $x^2+2x-3\neq 0$ ⇒ $x\neq -3;$ $x\neq 1$

$\frac{|x+4|-|x|}{x-1}0$

Подмодульные выражения обращаются в 0 в точках

x=-4 и x=0

Это точки делят числовую прямую на три промежутка.

Раскрываем знак модуля на промежутках:

(-∞;-4]

|x+4|=-x-4

|x|=-x

$\frac{-x-4-(-x)}{x-1}0$ ⇒ $\frac{-4}{x-1}0$ ⇒ x < 1

решение неравенства (-∞;-4]

(-4;0]

|x+4|=x+4

|x|=-x

$\frac{x+4-(-x)}{x-1}0$ ⇒ $\frac{2x+4}{x-1}0$ ⇒ x < -2 или x > 1

решение неравенства (-4;-2)

(0;+∞)

|x+4|=x+4

|x|=x

$\frac{x+4-x}{x-1}0$ ⇒ $\frac{4}{x-1}0$ ⇒ x > 1

решение неравенства (1;+∞]

Объединяем ответы трех случаев:

$\frac{|x+4|-|x|}{x-1}0$ при $x \in (-\infty;-2)\cup(1;+\infty)$

ОДЗ:

$\left \{ {{x\in (-\infty;-1-\sqrt{3}) \cup{-1+\sqrt{3};+\infty)} \atop{ {x\neq-3; x\neq 1 }\atop{ x \in (-\infty;-2)\cup(1;+\infty)}} \right.$

$x\in (-\infty;-3)\cup(-3;1-\sqrt{3}) \cup(1;+\infty)$

Решаем неравенство: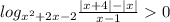 $log_{x^2+2x-2}\frac{|x+4|-|x|}{x-1}0$

$0=log_{x^2+2x-1}1$

$log_{x^2+2x-2}\frac{|x+4|-|x|}{x-1}log_{x^2+2x-2}1$

Два случая:

если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента

$\left \{ {{x^2+2x-21} \atop {\frac{|x+4|-|x|}{x-1}1}} \right.$ ⇒ $\left \{ {{x^2+2x-30} \atop {\frac{|x+4|-|x|-x+1}{x-1}0}} \right.$ ⇒ $\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.$

второе неравенство решаем на промежутках так:

(-∞;-4]

$\frac{-x-4-(-x)-x+1}{x-1}0$ ⇒ $\frac{-3-x}{x-1}0$ ⇒ $\frac{x+3}{x-1}$ ⇒ (-3;-1)

не принадлежат (-∞;-4]

на (-4;0]

$\frac{x+4-(-x)-x+1}{x-1}0$ ⇒ $\frac{x+5}{x-1}0$ ⇒ x < -5 или x > 1

не принадлежат (-4;0]

(0;+∞)

$\frac{x+4-x-x+1}{x-1}0$ ⇒ $\frac{5-x}{x-1}0$ ⇒ $\frac{x-5}{x-1}$ ⇒ $x\in (1;5)$

о т в е т этого случая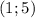 (1;5)

если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента

$\left \{ {{0$ ⇒ $\left \{ {0$ ⇒ $\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.$

второе неравенство решаем на промежутках так:

(-∞;-4]

$\frac{-x-4-(-x)-x+1}{x-1}$ ⇒ $\frac{-3-x}{x-1}$ ⇒ $\frac{x+3}{x-1}0$ ⇒

(-∞;-3)U(1;+∞)

о т в е т. (-∞;-4]

на (-4;0]

$\frac{x+4-(-x)-x+1}{x-1}$ ⇒ $\frac{x+5}{x-1}$ ⇒ -5 < x < 1

о т в е т. (-4;0]

(0;+∞)

$\frac{x+4-x-x+1}{x-1}$ ⇒ $\frac{5-x}{x-1}$ ⇒ $\frac{x-5}{x-1}0$ ⇒ $x\in (0;1)\cup(5;+\infty)$

о т в е т этого случая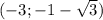 $(-3;-1-\sqrt{3})$

С учетом ОДЗ получаем окончательный ответ: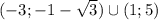 $(-3;-1-\sqrt{3})\cup(1;5)$

0,0(0 оценок)

Ответ:

KarinaKostolevskaya

17.04.2020 03:23

Раскрываем скобки. Для этого, значение перед скобками умножаем на каждое значение в скобках, и складываем их в соответствии с их знаками. То есть получаем:

2 * 1 - 2 * sin ^ 2 x = 1 - sin x;

2 - 2 * sin ^ 2 x = 1 - sin x;

Перенесем все значения выражения на оду сторону. При переносе значений, их знаки меняются на противоположный знак. То есть получаем:

2 * sin ^ 2 x - sin x + 1 - 2 = 0;

2 * sin ^ 2 x - sin x - 1 = 0;

1) sin x = 1;

x = pi/2 + 2 * pi * n, где n принадлежит Z;

2) sin x = - 1/2;

x = (- 1) ^ n * 7 * pi/6 + pi * n, где n принадлежит Z.

Объяснение:

0,0(0 оценок)

Популярные вопросы: Алгебра