Установите верность или неверность данных выражений. Функция. задашая формудой |у х называется линейной. Графики линейных функций ... если угловые коэффициенты равны, а свободные члены не равны пересекаются Графики линейных функций если параллельны угловые коэффициенты не равны График функции у3 x+b верно проходит через начало координат. ложь
Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру уравнение в действительных корнях.
Рассмотрим функцию . Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию . Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
ВвоыоФункция arcsin(x) обозначает угол, синус которого равен х. Это можно записать математически: sin(arcsin(x))=x. Справедливо и обратное: arcsin(sin(x))=x. Функция arcsin(x) - нечетная, как и обратная ей функция sin(x). Это значит, что arcsin(-x) = - arcsin(x). Поэтому arcsin(-3/4) = -arcsin(3/4). В принципе, arcsin(3/4) - это иррациональное число, выражающее некоторый вполне конкретный угол, заданный именно таким выражением. Но если тебя не устраивает такая запись, можно найти приближенное значение при инженерного калькулятора
Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру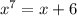 уравнение в действительных корнях.
уравнение в действительных корнях.
Рассмотрим функцию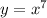 . Эта функция является возрастающей на всей числовой прямой.
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию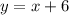 . Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение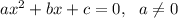
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
Это можно записать математически: sin(arcsin(x))=x.
Справедливо и обратное: arcsin(sin(x))=x.
Функция arcsin(x) - нечетная, как и обратная ей функция sin(x).
Это значит, что arcsin(-x) = - arcsin(x).
Поэтому
arcsin(-3/4) = -arcsin(3/4).
В принципе, arcsin(3/4) - это иррациональное число, выражающее некоторый вполне конкретный угол, заданный именно таким выражением. Но если тебя не устраивает такая запись, можно найти приближенное значение при инженерного калькулятора