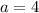В арифметической прогрессии S1000=S2021 Найдите S3021

а) Так как знаменатели дробей равны, можем приравнять числители:

х² = 5х - 6

х² - 5х + 6 = 0, получили квадратное уравнение. Ищем корни.

х первое, второе = (5 + - √25-24) : 2

х первое = 6 : 2 = 3       х второе = 4 : 2 = 2

b) Здесь немного изменим знаменатель, чтобы приравнять числители:

5 - х = -х + 5 = - (х - 5)

Подставляем изменённый второй знаменатель во вторую дробь, она сразу становится со знаком -

Сейчас можно приравнять числители.

х² - 6х = -5

х² - 6х + 5 = 0 Получили квадратное уравнение, ищем корни:

х первое, второе = (6 + - √36 -20) : 2

х первое = 10 : 2 = 5       х второе = 2 : 2 = 1

c) Решено верно, проверено)

Объяснение:

и

Объяснение:

Первый модуль обращается в ноль при x=-2, второй - при .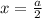

Пусть сначала

Тогда уравнение принимает вид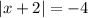 и, очевидно, не имеет решений.

Пусть теперь

Если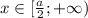 , то оба модуля раскрываются с плюсом и уравнение принимает вид:

Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если удовлетворяет системе неравенств

Решение системы: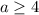

Если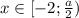 , то уравнение принимает вид

Полученный x будет корнем уравнения, если удовлетворяет системе:

Решение системы: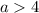

Пусть, наконец,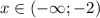 . Тогда уравнение принимает вид

Полученный x будет корнем уравнения, если удовлетворяет системе:

Эта система не имеет решений.

Теперь пусть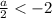 , то есть .

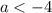Если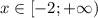 , то

Система:

Нет решений.

Если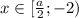 , то

Система:

Решение системы: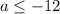

И наконец, если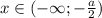 , то

Система:

Решение: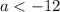

Из вышесказанного очевидно, что

При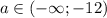 - два решения

При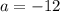 - одно решение

При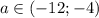 - нет решений

При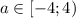 - нет решений

При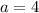 - одно решение

При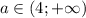 - два решения

Таким образом, уравнение имеет одно решение пр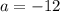и и