заключается в том, что необходимое выражение преобразуется с использованием основного логарифмического тождества.
Рассмотрим уравнение:
Основания степеней разные, но мы можем, например число представить в виде степени с основанием :
Тогда уравнение примет вид:
В правой части применяем одно из свойств степени:
Теперь мы получили в обеих частях уравнения степени с одинаковым основанием. Такое уравнение решается стандартным приемом путем перехода к уравнению:
заключается в том, что необходимое выражение преобразуется с использованием основного логарифмического тождества.
Рассмотрим уравнение:
Основания степеней разные, но мы можем, например число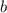 представить в виде степени с основанием
представить в виде степени с основанием  :
:
Тогда уравнение примет вид:
В правой части применяем одно из свойств степени:
Теперь мы получили в обеих частях уравнения степени с одинаковым основанием. Такое уравнение решается стандартным приемом путем перехода к уравнению: