Парабола. Ветви направлены вверх.
Вершина Фокус
Ось симметрии:
Направляющая:
Возрастает на: (;+∞)
Убывает на: (-∞;)
Функция не является четной или нечетной.
y=2·x2-3·x+7
(3)' = 2·x2-3·x+7((4·x-3)'·7+(4·x-3)·(7)') = 2·x2-3·x+7(2·7+(4·x-3)·(-3·x))
ответ: 4x-3
Пересекает ось при
Возрастает на: (−1;+∞)
Убывает на: (−∞;−1)
y=3·x2+6·x-4
(3·x2+6·x-4)' = (3·x2)' + (6·x)' + (-4)' = 6·x + 6 = 6·x+6
Производную этого выражения находим по формуле: (xn)' = n*xn-1
(3·x2)' = 3·2·x2-1(x)' = 6·x
(x)' = 1
ответ: 6x+6
Объяснение:
Упростим выражение (х - 5)^2 - х(10 + х) и найдем его значение при x = - 1/20.
Откроем скобки в выражении. Первую скобку открыть формула сокращенного умножения — квадрат разности (a - b)^2 = a^2 - 2ab + b^2;
Вторую скобку мы откроем при дистрибутивного закона умножения и правила открытия скобок перед которыми стоит знак минус.
(x - 5)^2 - x(10 + x) = x^2 - 10x + 25 - 10x - x^2 = - 10x - 10x + 25 = - 20x + 25;
Найдем значение выражения при x = - 1/20:
- 20x + 25 = - 20 * (- 1/20) + 25 = 1 + 25 = 26.
Парабола. Ветви направлены вверх.
Вершина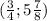 Фокус
Фокус 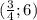
Ось симметрии: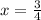
Направляющая: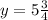
Возрастает на: (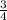 ;+∞)
;+∞)
Убывает на: (-∞;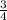 )
)
Функция не является четной или нечетной.
y=2·x2-3·x+7
(3)' = 2·x2-3·x+7((4·x-3)'·7+(4·x-3)·(7)') = 2·x2-3·x+7(2·7+(4·x-3)·(-3·x))
ответ: 4x-3
Парабола. Ветви направлены вверх.
Вершина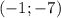 Фокус
Фокус 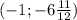
Ось симметрии: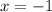
Направляющая: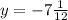
Пересекает ось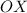 при
при 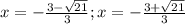
Возрастает на: (−1;+∞)
Убывает на: (−∞;−1)
Функция не является четной или нечетной.
y=3·x2+6·x-4
(3·x2+6·x-4)' = (3·x2)' + (6·x)' + (-4)' = 6·x + 6 = 6·x+6
Производную этого выражения находим по формуле: (xn)' = n*xn-1
(3·x2)' = 3·2·x2-1(x)' = 6·x
(x)' = 1
ответ: 6x+6
Объяснение:
Упростим выражение (х - 5)^2 - х(10 + х) и найдем его значение при x = - 1/20.
Откроем скобки в выражении. Первую скобку открыть формула сокращенного умножения — квадрат разности (a - b)^2 = a^2 - 2ab + b^2;
Вторую скобку мы откроем при дистрибутивного закона умножения и правила открытия скобок перед которыми стоит знак минус.
(x - 5)^2 - x(10 + x) = x^2 - 10x + 25 - 10x - x^2 = - 10x - 10x + 25 = - 20x + 25;
Найдем значение выражения при x = - 1/20:
- 20x + 25 = - 20 * (- 1/20) + 25 = 1 + 25 = 26.