Посчитаем сначала количество чисел, записываемых цифрами от до , а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
Выпишем числа от до : . Любые вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть: .
Теперь посчитаем количество тех, в которых есть четыре подряд идущих. В этом случае мы можем вычеркивать только из -ех оставшихся чисел. Поскольку четверок подряд идущих , то всего искомых чисел .
Посчитаем сначала количество чисел, записываемых цифрами от до
до 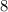 , а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
, а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
Выпишем числа от до
до 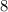 :
: 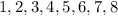 . Любые
. Любые 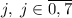 вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть:
вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть: 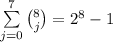 .
.
Теперь посчитаем количество тех, в которых есть четыре подряд идущих. В этом случае мы можем вычеркивать только из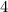 -ех оставшихся чисел. Поскольку четверок подряд идущих
-ех оставшихся чисел. Поскольку четверок подряд идущих 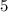 , то всего искомых чисел
, то всего искомых чисел 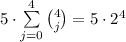 .
.
Итого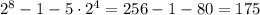 .
.
3x + 2y = 8;
2x + 6y = 10,
применим метод подстановки. И начнем мы с того, что второе уравнение разделим на 2 и получим:
3x + 2y = 8;
x + 3y = 5.
Выражаем из второго уравнения переменную x:
x = 5 - 3y;
3x + 2y = 8.
Подставляем вместо x выражение из первого уравнения.
x = 5 - 3y;
3(5 - 3y) + 2y = 8.
Решаем первое уравнение системы:
3 * 5 - 3 * 3y + 2y = 8;
15 - 9y + 2y = 8;
-9y + 2y = 8 - 15;
-7y = -7;
y = 1.
Система уравнений:
x = 5 - 3 * 1 = 5 - 3 = 2;
y = 1.