В экзаменационную работу входят программный материал первой и второй четверти. Первое задание выполните действия в примере а вы должны привезти все дроби к общему знаменателю найти дополнительные множители к каждой из дробей затем в числителе привести подобные слагаемые и если получится сократимая дробь её необходимо сократить. Второй пример первого задания выполняем по действиям, первое действие выполняется в первое скобки, второе действие выполняется во второй скобки и третье действие это будет деление. Второе задание сократите дроби ВВ примерах Аиб вы просто делите на наибольший общий делитель и числитель и знаменатель. В примерах Виг для того чтобы сократить эти дроби Вы должны в знаменательях этих дробей вынести за скобку общий множитель применить формулу сокращенного умножения для числителя в примере Ви только затем можете сокращать.
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, , но сейчас это не нужно), нам повезло, это 32
Учитываем, что , получаем
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
Остаток 21, чудесно. Выполняем последний шаг.
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
7х-2у=0 запишем как уранение прямой с угловым коэффициентом k: y=3,5x Прямая проходит через точки (0;0) и (2;7)
3х+6у=24 запишем в виде уравнения в отрезках. Для этого делим каждое слагаемое на 24. (х/8)+(у/4)=1 Легко построить прямую. Она отсекает на осях координат отрезки: на оси ох длиной 8; на оси оу длиной 4. Прямая проходит через точки (8;0) и (0;4). См. графическое решение в приложении.
Решение сложения Умножаем первое уравнение на 3: 21х-6у=0 3х+6у=24 Складываем 24х=24 ⇒ х=1 у=3,5х=3,5·1=3,5
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,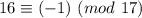 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что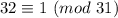 , получаем
, получаем
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
Остаток 21, чудесно. Выполняем последний шаг.
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
y=3,5x
Прямая проходит через точки (0;0) и (2;7)
3х+6у=24 запишем в виде уравнения в отрезках. Для этого делим каждое слагаемое на 24.
(х/8)+(у/4)=1
Легко построить прямую. Она отсекает на осях координат отрезки:
на оси ох длиной 8;
на оси оу длиной 4.
Прямая проходит через точки (8;0) и (0;4).
См. графическое решение в приложении.
Решение сложения
Умножаем первое уравнение на 3:
21х-6у=0
3х+6у=24
Складываем
24х=24 ⇒ х=1 у=3,5х=3,5·1=3,5
О т в е т. (1;3,5)