В коробке лежат 20 компьютерных чипов, 4 из которых бракованные. Необходимо определить вероятность того, что дважды наудачу вытаскивают из коробки чип , обнаруживают что он бракованный.

а)2

б)1

в)3

г) если 5 это ∅ то правильный ответ 5

Объяснение:

а)Переносишь 4 на другую сторону уравнения

х2>-4

А так как степенная функция с парным показателем всегда либо положительная либо 0

То х любое число

б)Так же переносишь 4

Дальше получается х2>4

Тогда |x|>2

x>2,x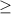0

-x>2,x<0

Находим пересечение:

x∈(2,+∞)

x∈(-∞,-2)

в)Как обычно переносим 4

Получается:x2<4

|x|<2

Рассматриваешь все случаи:

x<2,x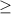0

-x<2,x<0

Находишь пересечение:

x∈[0,2)

x∈(-2,0)

Объединяешь:x∈(-2,2)

г)Переносишь 4:

х2<-4

А это невозможно по этому ∅

Відповідь: a) (-1; -4) b) x=-1 с) ОХ: (-1+√2; 0) и (-1-√2; 0) OY: (0; -2) e) в I, II, III и IV четвертях

Пояснення:

a) x=-b/2a x=-4/4=-1 y=-4

b) ось симметрии параболы - прямая, проходящая через её вершину (-1;-4) и параллельная оси Оу, поэтому абцисса ( х ) в любой точке на этой прямой одинакова и равна -1 => х = -1

c) при пересечении с осью ОХ ордината y=0 => 2x^2+4x-2=0

x1=-1+√2 x2=-1-√2

при пересечении с осью OY абсцисса х=0 y=-2

e) ветви параболы направлены вверх т.к. коэффициент а больше 0 а=2.Расположена она во всех 4-ёх четвертях