Числа, которые при делении на 12 дают остаток 5, имеют вид: 12k + 5, где k ∈ N. Для трёхзначных чисел выполняется двойное неравенство: 100 ≤ 12k + 5 ≤ 999, или 95 ≤ 12k ≤ 994, или Т.о. при 8 ≤ k ≤ 82, или 96 ≤ 12k ≤ 984, или 101 ≤ 12k + 5 ≤ 989, мы получаем все трёхзначные числа, которые при делении на 12 дают остаток 5. Всего таких чисел 82 - 8 + 1 = 75. Итак, мы знаем первое и последнее число арифметической прогрессии с шагом, равным 12, и количество таких членов. Поэтому спокойно можем использовать формулу суммы арифметической прогрессии: Подставляем свои значения и считаем:
12k + 5, где k ∈ N. Для трёхзначных чисел выполняется двойное неравенство:
100 ≤ 12k + 5 ≤ 999, или 95 ≤ 12k ≤ 994, или
Т.о. при 8 ≤ k ≤ 82, или 96 ≤ 12k ≤ 984, или 101 ≤ 12k + 5 ≤ 989, мы получаем все трёхзначные числа, которые при делении на 12 дают остаток 5. Всего таких чисел 82 - 8 + 1 = 75.
Итак, мы знаем первое и последнее число арифметической прогрессии с шагом, равным 12, и количество таких членов. Поэтому спокойно можем использовать формулу суммы арифметической прогрессии:
Подставляем свои значения и считаем:
1)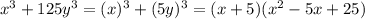
рассмотрим обратный пример
===========================================================
2)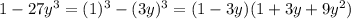
рассмотрим обратный пример
===========================================================
3)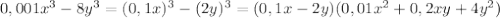
===========================================================
4)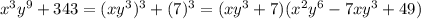
Вам на придут формулы сокращённого умножения
Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов.
===================================================================
Произведение разности двух величин на неполный квадрат суммы равно разности их кубов.