В квадрат, сторона которого равна 20 см, вписан другой квадрат, вершины которого являются серединами сторон первого квадрата, в этот квадрат вписан таким же образом другой квадрат, и т. д. (см. рис.).
Вычисли сумму площадей всех квадратов.
Сумма площадей всех квадратов равна
см2
Дополнительные во сторона третьего по порядку квадрата равна
см.
2. Площадь наибольшего квадрата равна
см2.
3. Знаменатель равен
.
4. Выбери, какую из формул надо использовать в решении задачи:
b1(1−qn)1−q
b11−q
(b1+b2)q2
b11−q2
Т.к под корнем не может быть отрицательного значения х+1>0; => х> -1
Возведем в квадрат обе стороны:
√(х+1) ≥ х√2
х+1≥2х²
Перенесем все в левую часть, меняя знак на противоположный:
-2х²+х+1≥0
Домножим на -1 обе части, сменив при этом знак неравенства на противоположный:
2х²-х-1≤0
Приравняем к нулю, чтобы найти корни через Дискриминант:
2х²-х-1=0
Д=(-1)²-4*2*(-1)= 1+8= 9
х1,2= (1±3)/4
х1=1
х2=-0.5
Начертим ось х, и отметим 2 точки: -0.5 и 1, получим: (Смотри рисунок)
Вернемся к Одз:
х принадлежит [-1; 1]
ответ: х принадлежит [-1; 1]
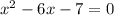
Найти:Значение квадратного уравнения.
Решение:для 8 класса (через дискриминант):
Вспоминаем вид уравнения, при котором можно вычислить дискриминант: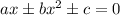
.
То есть наше уравнение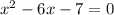
, где 
, 
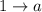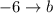и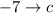 
.
Вспоминаем формулу нахождения дискриминанта: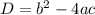
.
⇒
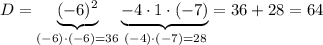
Вы (очень надеюсь) знаете, что есть правила дискриминанта:
Поскольку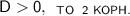
Вспоминаем формулу нахождения корней уравнения:
для 7 класса (через разложение трёхчлена):
Представим член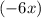
в виде выражения 
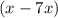и запишем его в уравнение:
Произведение равно 0, если один из множителей равен 0.
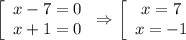
ответ: