В равнобедренном треугольнике с длиной основания 55 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD. Рассмотрим треугольники ΔABD и Δ (треугольник записать в алфавитном порядке);
1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ A = ∡ ;
2. так как проведена биссектриса, то ∡ = ∡ CBD;
3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC — .
По второму признаку равенства треугольников ΔABD и ΔCBD равны.Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам. AD=
25
Объяснение:
решения.
Выпишем несколько первых натуральных чисел кратных 5:
5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).
Пронумеруем члены последовательности:
Число, следующее за четвертым членом последовательности 25.
решения.
Воспользуемся формулой для нахождения n-го члена арифметической последовательности.
Наименьшее натуральное число делящееся на 5 это 5, т.е.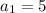 .
.
Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е.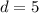 .
.
Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.
Рабочие производили детали 17 дней и произвели 1156 деталей.
Объяснение:
Допустим x - максимальное количество дней. Тогда x-2 - это количество затраченных дней.
(x-2)*68 = 60x - если производить 68 деталей в день x-2 дней, то получится то же кол-во, если производить 60 деталей x дней.
Решаем уравнение
68x-136 = 60x
68x - 60x = 136
8x = 136
x = 136/8
x = 17
ответ: на изготовление деталей ушло 17 дней.
Рабочие 17 дней производили 68 деталей в день. Значит кол-во деталей равно 17*68
17*68 = 1156
ответ: 1156 деталей произвели рабочие.
Если есть вопросы, пиши