. Первого игрока команды можно выбрать среди 15 спортсменов, то есть . Второго игрока команды можно выбрать среди оставшийся 14 спортсменов, то есть . Точно также, третьего игрока команды можно выбрать , четвёртого игрока команды можно выбрать , и наконец, пятого игрока команды можно выбрать .
Однако каждая команда при этом подсчете учтена несколько раз: одна и та же пятёрка спортсменов может быть выбрана по разному, например, сначала А, потом В, потом С, потом D, потом E, или сначала B, потом А, потом C, потом D, потом E и так далее. Поскольку число перестановок из пяти элементов равно 5!=120, то каждая команда учтена нами ровно 120 раз. Поэтому получается, что команду из 5 игроков можно выбрать
.
. Применим формулу комбинаторики.
Определение. Пусть имеется множество, содержащее n элементов. Произвольный неупорядоченный набор, состоящий из k различных элементов данного множества, называется сочетанием из n элементов по k элементов (или просто сочетанием из n по k).
Число сочетаний из n элементов по k элементов обозначается и вычисляется по формуле:
Выражение под корнем всегда должно быть неотрицательным, значит, х ≥ 0. Теперь возводим в квадрат обе части уравнения (1):
х = 1, смотрим на неравенство, х = 1 ≥ 0, значит, х = 1 – решение уравнения.
2. √х = -х - 2 (2)
Делаем то же самое. Выражение под корнем должно быть неотрицательным, но также в правой части уравнения (2) есть переменная, и правая часть тоже принимает разные значения, но извлечение корня из неотриц. выражения – так же неотриц. значение. Поэтому нужно, чтобы два условия выполнялись одновременно, т.е. нужно составить систему неравенств:
х ≥ 0
-х - 2 ≥ 0 (все это в системе)
Отсюда:
х ≥ 0
х ≤ -2 (в системе)
Могут ли эти условия выполняться одновременно? Т.е. есть ли такой х = числу, которое больше нуля и меньше -2? Такого числа не существует, значит, решения уравнени не сущ., следует, х принадлежит пустому множеству.
Объяснение:
Задачу можно решить различными .
. Первого игрока команды можно выбрать среди 15 спортсменов, то есть . Второго игрока команды можно выбрать среди оставшийся 14 спортсменов, то есть . Точно также, третьего игрока команды можно выбрать , четвёртого игрока команды можно выбрать , и наконец, пятого игрока команды можно выбрать .
Однако каждая команда при этом подсчете учтена несколько раз: одна и та же пятёрка спортсменов может быть выбрана по разному, например, сначала А, потом В, потом С, потом D, потом E, или сначала B, потом А, потом C, потом D, потом E и так далее. Поскольку число перестановок из пяти элементов равно 5!=120, то каждая команда учтена нами ровно 120 раз. Поэтому получается, что команду из 5 игроков можно выбрать
.
. Применим формулу комбинаторики.
Определение. Пусть имеется множество, содержащее n элементов. Произвольный неупорядоченный набор, состоящий из k различных элементов данного множества, называется сочетанием из n элементов по k элементов (или просто сочетанием из n по k).
Число сочетаний из n элементов по k элементов обозначается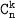
и вычисляется по формуле:
Так как n = 15 и k = 5, то
1. √х = 1 (1)
Выражение под корнем всегда должно быть неотрицательным, значит, х ≥ 0. Теперь возводим в квадрат обе части уравнения (1):
х = 1, смотрим на неравенство, х = 1 ≥ 0, значит, х = 1 – решение уравнения.
2. √х = -х - 2 (2)
Делаем то же самое. Выражение под корнем должно быть неотрицательным, но также в правой части уравнения (2) есть переменная, и правая часть тоже принимает разные значения, но извлечение корня из неотриц. выражения – так же неотриц. значение. Поэтому нужно, чтобы два условия выполнялись одновременно, т.е. нужно составить систему неравенств:
х ≥ 0
-х - 2 ≥ 0 (все это в системе)
Отсюда:
х ≥ 0
х ≤ -2 (в системе)
Могут ли эти условия выполняться одновременно? Т.е. есть ли такой х = числу, которое больше нуля и меньше -2? Такого числа не существует, значит, решения уравнени не сущ., следует, х принадлежит пустому множеству.