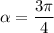В школе провели олимпиаду по математике среди 64 учащихся восьмых классов. Каждое задание оценивалось от 0 до Сумма , набранных всеми участниками, составила 352. Известно, что:

- в 8А классе в олимпиаде приняли участие 24 человека, среднее арифметическое набранных равно 4,5;

- средний учащихся 8Б класса равен 5,5;

- средний учащихся 8В класса является целым числом;

- количество участников олимпиады от каждого класса не превышало 30 человек.

Найдите количество учащихся 8В класса, принявших участие в олимпиаде.

ЗАПИШИТЕ РЕШЕНИЕ И ОТВЕТ

За интеграл я буду Июиспользовать вот этот знак:

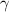
1) Перепишите дробь:

2) Использовать свойства интегралов:

3) Вычислить интегралы и прибавить константу интегрирования С:

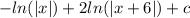
1) Найти неопределённый интеграл:

2) Упростить интеграл, используя метод замены переменной:

3) Преобразовать выражения:

4) Вычислить произведение:

5) Использовать свойство интегралов:

6) Вычислить интегралы:

7) Выполнить обратную замену:

8) Упростить выражение:

9) Вернуть пределы интегрирования и подставить в пример (8):

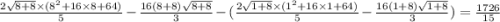
Найдем уравнение касательной, проходящей через точку с абсциссой

Для этого найдем производную данной функции:

Найдем значение функции в точке с абсциссой :

Найдем значение производной данной функции в точке с абсциссой :

Уравнение касательной имеет вид:

Подставим значение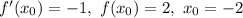

Итак, уравнение касательной заданной функции: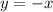

Воспользуемся геометрическим смыслом касательной: коэффициент наклона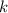 касательной 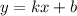численно равен тангенсу угла наклона  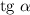с положительным направлением оси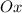

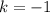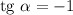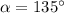В найденной касательной коэффициент , следовательно, при или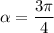

ответ: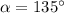 или