В школе введен дистанционный режим, при котором есть самоподготовка и конференции. известно что с вероятность. 0,8 тип уроков завтра будет таким же как и сегодня. сегодня 20 мая и в школе проводятся конференции. найдите вероятность того, что 23 мая в школе будут проходить уроки самоподготовки
Общая схема исследования функции:
Найти ОДЗ и точки разрыва функции. Найти точки пересечения графика функции с осями координат. Провести исследование функции с первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания. Исследовать функцию с производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости. Найти асимптоты графика функции: а) вертикальные, b) наклонные. На основании проведенного исследования построить график функции.1. Здесь функция ограничений не имеет, точек разрыва тоже не имеет, т.е. существует для всех действительных х. Область определения функции: D(f) = R
2. Точки пересечения с осями координат.
2.1. Точки пересечения с осью абсцисс
Чтобы найти точки пересечения с осью Ох, нужно принять y=0:
2.2. Точки пересечения с осью ординат.
Здесь нужно принять x=0 и подставив в функцию, получим y=2
3. Найдем производную функции
Приравниваем производную функции к нулю
___-____(-1)____+___(1)_____-__
Функция возрастает на промежутке (-1;1), а убывает - (-∞;-1) и (1;+∞). В точке х=-1 производная функции меняет знак с (-) на (+), следовательно, точка х=-1 имеет локальный минимум, а в точке x=1 производная функции меняет с (+) на (-), имеем локальный максимум в точке х=1.
Найдем теперь вторую производную
(0;2) - точка перегиба
Вертикальной асимптоты нет.
Поскольку предел f(x) и f(x)/x при х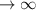 равен
равен 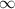 , то горизонтальной и наклонной асимптот нет.
, то горизонтальной и наклонной асимптот нет.
2) С непосредственной подстановкой я думаю все ясно. А выполнить проверку с схемы Горнера можно найдя остаток от деления исходного многочлена на (x-x0) (ведь по теореме Безу и будет значением многочлена в точке x0). Схему Горнера тут неудобно оформлять, поэтому давай сам как нибудь.
3) В соответствии с теоремой о рациональных корнях многочлена с целыми коффициентами, целые корни должны быть делителями свободного члена 3.
Делители тройки: 1, -1, 3, -3. Убеждаемся что только числа 1 и 3 являются корнями. ответ: x=1, x=3
4) Сначала поищем целые корни. Проверим числа 1, -1, 3, -3, 9, -9. 1 - корень, поэтому делим исходный многочлен на (x-1) и получаем
5x^2+14x+9. Теперь решаем квадратное уравнение находим еще два корня x=-9/5 и x=-1
Таким образом 5x^3+9x^2-5x-9=(x-1)(x+1)(5x+9)