в соревнования по танковому биатлону участвует 12 команд.С жребия их нужно разделить на 3 группы по 4 команды в каждой. в ящике в перемешку ляжат карточки с номерами гРупп :1,1,1,1,2,2,2,2,3,3,3,3. капитан команд тянут по одной карточке. Какова вероятность того, что команда Казахстана окажется во 2ой группе?
Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая: .
Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент k .
Линейная функция задаётся уравнением .
Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид
Найдём число "b" , подставив координаты точки D(7;-10) в уравнение линейной функции.
ответ:Одна из сторон прямоугольника равна 12 см, а дина второй 12 - 4 = 8 см.
Объяснение:
Нам задан прямоугольник площадь которого равна 96 см^2. Нужно найти длины сторон этого прямоугольника, если известно, что одна из них на 4 см меньше другой.
Давайте введем переменную. Пусть x см — длина одной стороны прямоугольника, тогда длина второй стороны равна (x - 4) см.
Вспомним формулу для нахождения площади прямоугольника:
S = a * b;
x * (x - 4) = 96;
x^2 - 4x = 96;
x^2 - 4x - 96 = 0;
D = b^2 - 4ac = 16 - 4 * (-96) = 16 + 384 = 400;
x1 = (4 + 20)/2 = 24/2 = 12;
x2 = (4 - 20)/2 = -16/2 = -8.
Одна из сторон прямоугольника равна 12 см, а дина второй 12 - 4 = 8 см.
ответ: y= -3x+11 .
Уравнение функции, описывающей прямо пропорциональную зависимость между переменнными "х" и "у" , такая: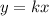 .
.
Подставим координаты точки А(-4;12) в это равенство и найдём коэффициент k .
Линейная функция задаётся уравнением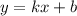 .
.
Так как график линейной функции параллелен графику прямой пропорциональности, то у этих функций будут равные угловые коэффициенты, то есть линейная функция будет иметь вид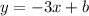
Найдём число "b" , подставив координаты точки D(7;-10) в уравнение линейной функции.
ответ:Одна из сторон прямоугольника равна 12 см, а дина второй 12 - 4 = 8 см.
Объяснение:
Нам задан прямоугольник площадь которого равна 96 см^2. Нужно найти длины сторон этого прямоугольника, если известно, что одна из них на 4 см меньше другой.
Давайте введем переменную. Пусть x см — длина одной стороны прямоугольника, тогда длина второй стороны равна (x - 4) см.
Вспомним формулу для нахождения площади прямоугольника:
S = a * b;
x * (x - 4) = 96;
x^2 - 4x = 96;
x^2 - 4x - 96 = 0;
D = b^2 - 4ac = 16 - 4 * (-96) = 16 + 384 = 400;
x1 = (4 + 20)/2 = 24/2 = 12;
x2 = (4 - 20)/2 = -16/2 = -8.
Одна из сторон прямоугольника равна 12 см, а дина второй 12 - 4 = 8 см.