В течение года 24 знатока участвовали в передаче «Своя игра». В одной игре участвует ровно 3 из них. Назовём пару знатоков уникальной, если в этом году они играли друг с другом ровно один раз. В конце года оказалось, что в каждой тройке игроков есть хотя бы одна уникальная пара. Какое наибольшее количество игр могло быть сыграно в этом году?

 - красные

  - жёлтые

  - все шары

   все шары без одного, т.е. все оставшиеся.

По условию:      .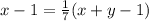

Получаем первое уравнение:

Ещё по условию:   .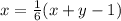

Второе уравнение:    

Левые части обоих уравнений равны, значит, их правые части равны между собой.

                     красныx шаров в коробке.

Подставим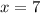    в уравнение  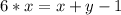   и получим:

                      жёлтыx шаров в коробке.

         всего шаров в коробке.

ответ:     7  красныx;

               36  жёлтых;

                43 всего шаров в коробке.  

2,5

Объяснение:

Обозначим скорость Лады L км/ч, а скорость Мерседеса M км/ч.

Путь обозначим AB = S км. Так как они встретились через 8 ч, то:

M + L = S/8

Если бы скорость Мерседеса была 1,14M км/ч, а скорость Лады 1,15L км/ч, то они встретились бы через 7 ч:

1,14M + 1,15L = S/7

Получили систему, в которой 2 уравнения и 3 неизвестных.

Умножаем 1 уравнение на 8, а 2 уравнение на 7

{ 8M + 8L = S

{ 7,98M + 8,05L = S

Правые части равны, приравниваем левые части друг к другу.

8M + 8L = 7,98M + 8,05L

8M - 7,98M = 8,05L - 8L

0,02M = 0,05L

2M = 5L

M : L = 5/2 = 2,5