Общее количество вариантов выбрать 2 шара из 6 имеющихся равно числу сочетаний из 6 по 2:
Определим сколькими можно выбрать два шара одного цвета. Так как черный шар всего один, то это могут быть либо белые шары, либо красные. Выбрать 2 белых шара можно , а 2 красных шара - .
Вероятность определим как отношение благоприятных вариантов к общему числу вариантов:
Определим сколькими можно выбрать два шара так, чтобы один из них был черным. Если один шар черный, то другой можем выбрать из пяти оставшихся шаров, то есть всего существует 5 благоприятных вариантов.
Общее количество вариантов выбрать 2 шара из 6 имеющихся равно числу сочетаний из 6 по 2:
Определим сколькими можно выбрать два шара одного цвета. Так как черный шар всего один, то это могут быть либо белые шары, либо красные. Выбрать 2 белых шара можно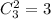 , а 2 красных шара -
, а 2 красных шара - 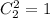 .
.
Вероятность определим как отношение благоприятных вариантов к общему числу вариантов:
Определим сколькими можно выбрать два шара так, чтобы один из них был черным. Если один шар черный, то другой можем выбрать из пяти оставшихся шаров, то есть всего существует 5 благоприятных вариантов.
Определяем вероятность: