Слова "пересечение с осями координат" означают, что нужно положить одну координату равной нулю (это ситуация соответствует пересечению с другой осью) и найти из получившегося уравнения оставшуюся неизвестную, затем провести аналогичную операцию со второй координатой (пересечение с другой осью).
Например, рассмотрим равенство . Чтобы определить в какой точке график такой функции пересекает абсциссу (ось х), нужно положить . Тогда получим, что , значит пересечение с осью x происходит в точке . Аналогично для оси ординат.
Если вы не представляете себе, как выглядит график линейной функции, попробуйте построить его по точкам.
ОДЗ первого неравенства находим из условия
х-2>0⇒x>2
x+2>0⇒x>-2
Значит, ОДЗ х>2, или х∈(2;+∞), а второго
(x-2)(x+x)>0 найдем решения методом интервалов.
х=2, х=-2,
-22
+ - +
х∈(-∞;-2)∪(2;+∞)
я ВЫДЕЛИЛ Вам жирным шрифтом ОДЗ, видите разницу? Так вот применение свойства
㏒ₐx+㏒ₐy=㏒ₐ(xy) расширяет область определения на интервал
(-∞;-2)
поэтому, решая первое неравенство системы, (x-3)*(x+3)>0
-33
+ - +
Вы получите лишний промежуток, а именно (-∞;-3), входящий в интервал (-∞;-2); его надо исключить из ответа.
Слова "пересечение с осями координат" означают, что нужно положить одну координату равной нулю (это ситуация соответствует пересечению с другой осью) и найти из получившегося уравнения оставшуюся неизвестную, затем провести аналогичную операцию со второй координатой (пересечение с другой осью).
Например, рассмотрим равенство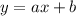
. Чтобы определить в какой точке график такой функции пересекает абсциссу (ось х), нужно положить 
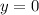. Тогда получим, что 
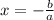, значит пересечение с осью x происходит в точке 
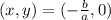. Аналогично для оси ординат.
Если вы не представляете себе, как выглядит график линейной функции, попробуйте построить его по точкам.