В заданиях №1 и №2 выберите один правильный ответ:
№1.Пусть материальная точка движется прямолинейно по закону s = 4t – 3, где s – путь, пройденный за время t. Найдите мгновенную скорость этой точки в момент времени t.
1) 4 2) 2 3) 1 4)3
№2.Дана функцияf(x) = – x2 + 1. Какие из приведённых выражений верны?
I) Тангенс угла наклона касательной в точке с абсциссой x = – 1 равен 2;
II) Значение производной в точке x = 1 равно (– 2);
III) Производная равна 1 приx = 1/2.
1) только II и III 2) только I и III 3) только I и II 4) I, II и III
№3.Вычислите значение производной функции f(x) в точке х0, если:
а) f(x) = (х – 3)2, х0 = 2 б) f(x) = 1/3х3 – 1/2х2 + 4х – 3, х0 = – 1
№4. В любой точкеx∈ Rнайдите производную функции:
а) у = (х – 1)(х + 1)(х2 + 1) в) у = 3x/(x^2+1)
б) у = (3х3 – 2х)(х2 + х + 5) г)у
Пусть вся дорога 1 (единица), тогда х время, за которое первая бригада может отремонтировать дорогу, а у время второй бригады. Совместная работа двух бригад 6 ч. Если первая бригада отремонтирует 3/5 дороги, то время затратит (3/5)÷(1/х)=3х/5 ; если вторая бригада отремонтирует оставшуюся часть: 1-3/5=2/5 дороги. то время затратит (2/5)÷(1/у)=2у/5 , и времени они затратят 12 часов. Составим два уравнения:
1/х+1/у=1/6
3х/5+2у/5=12
Выделим х во втором уравнении:
3х/5+2у/5=12
15х+10у=300
3х+2у=60
х=(60-2у)/3
Подставим значение х в первое уравнение:
3/(60-3у)+1/у=1/6
18у+360-12у=60у-2у²
2у²-54у+360=0
у²-27у+180=0
D=9
у₁=12 часов вторая бригада может отремонтировать дорогу самостоятельно.
х₁=(60-2*12)/3=36/3=12 часов первая бригада может отремонтировать дорогу самостоятельно.
у₂=15 часов вторая бригада может отремонтировать дорогу самостоятельно.
х₂=(60-2*15)/3=30/3=10 часов первая бригада может отремонтировать дорогу самостоятельно.
ответ: Или первая за 12 часов и вторая за 12 часов; Или первая за 10 часов и вторая за 15 часов.
Каноническое уравнение, задающее эллипс, выглядит так:
Перепишем уравнение эллипса, поменяв местами параметры и
и 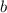 :
:
При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.
Найдём эксцентриситет:
Найдём фокальное расстояние (полурасстояние между фокусами):
Тогда расстояние между фокусами в два раза больше: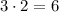 .
.
ответ: 6 ед.
На чертеже изображён данный эллипс.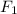 и
и 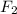 — его фокусы.
— его фокусы.