Вариант-1 1. Найдите значение корня: а) √9∗36; б) √16∗900; в) √0,64∗25; г) √0,49∗16.
2. Найдите значение выражения: а) √40∗490; б) √18∗32; в) √12,1∗0,4;
3. Найдите значение произведения: а) √2 * √18; б) √13 * √52;
4. Вычислите: а) √112+ 602; б) √852− 842;
5. Найдите значение корня: а) √4964; б) √925; в) √ 3 625;
6. Найдите значение частного: а) √8√50; б) √4,8√0,3.
7. Расположите в порядке убывания числа: 6; √21; 5; √40; и √35,8.
(см. объяснение)
Объяснение:
Введем функцию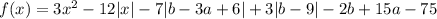 .
.
Заметим, что перед нами уравнение двух парабол, склеивающихся в фиксированной точке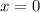 .
.
Этот график может ездить только вверх-вниз в зависимости от значений параметров и
и 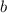 .
.
Уравнение может иметь ровно два корня при любом значении параметра
может иметь ровно два корня при любом значении параметра 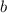 только, если
только, если 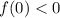 .
.
Тогда перейдем к неравенству:
Построим его в координатах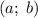 .
.
(см. прикрепленный файл)
Получили, что при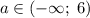 исходное уравнение имеет ровно два различных корня при любом значении параметра
исходное уравнение имеет ровно два различных корня при любом значении параметра 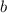 .
.
ответим теперь на вопрос задачи: ниже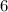 .
.
Задание выполнено!
Рисунок к задаче в прикрепленном файле.
Обозначим длины сосен отрезками: АВ = 12 м, СК = 30 м.
Расстояние между соснами обозначим отрезком АК = 24 м.
Проведем отрезок ВС. Длина этого отрезка равна расстоянию между верхушками сосен.
Геометрическая фигура, которая у нас получилась, прямоугольная трапеция (т.к. мы считаем в идеале, что сосны растут точно перпендикулярно земле, и поверхность земли горизонтальная).
АВСК прмоугольная трапеция с основаниями АВ и СК.
Проведем высоту ВН (см. рисунок).
АВНК - прямоугольник. АК=ВН=24, АВ=НК=12.
СН=СК-КН=30-12=18
Рассмотрим ΔВСН. Он прямоугольный, т.к. ВН⊥СК.
По теореме Пифагора
ВС² = ВН²+СН²
ВС² = 24²+18²=576+324=900
ВС = 30 (м)
ответ: расстояние между верхушками сосен 30 м.