І вариант 1. Выполните сложение:
7
12
15
7
е)
+
25
15
5 5
11
а) 15,6 - 28,7; в) 45,4 + (- 75, 3); д)
б) – 21,9+(- 23,6); г) 23,4 -(- 15,8);
2. Выполните вычитание:
а) 29,8 — 65,4; в) — 15,8 – 39,7; д)
д) —
21 28
5
б) 23,7 — — 14,8); г) — 24,6 — — 5,9); е)
42 4528
3. Раскройте скобки и выполните действия:
а) 78,9 + (- 13,6 — 105,6); б) 29,4 — (5,6 — 41,4).
4. Выполните действия:
- 1,6+ 23,1 + ( — 7,4) + (- 2,31).
5. Упростите выражение:
а) — 27,9 + (- 26, 3) + k; б) у+(- 13,6) + 18,4.
6. Решите уравнение:
а) – 5,9 + х = 6,9; б) п — 6 = — 15, 1.
Формула работы: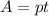
, р - производительность , t- время .
Если 6 насосов выкачивают воду из 1 бассейна за 10 часов, то за 1 час эти 6 насосов выкачают 1/10 часть бассейна. То есть производительность 6-ти насосов = 1/10 бассейна в час.
Производительность же 1 насоса равна (1/10):6=1/60 бассейна в час.
а) За 5 часов всю воду из 1 бассейна выкачают n насосов, то есть можно записать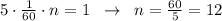
насосов.
За 15 часов всю воду из 1 бассейна выкачивают m насосов, то есть можно записать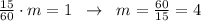
насоса.
б) Три насоса за 1 час выкачивают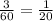
часть бассейна, значит всю воду из 1 бассейна три насоса выкачают за 
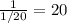часов.
9 насосов за 1 час выкачивают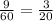
часть бассейна, значит всю воду из 1 бассейна 9 насосов выкачают за 
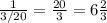часa.
а - первое число арифметической прогрессии
b - второе число арифметической прогрессии
c - третье число арифметической прогрессии
а+b+с = 9 -сумма членов ариф. прогрессии
Сумму членов ариф. прогрессии можно вычислить и по формуле
Sₓ = ((а+с)/2) * х
где х = 3 - количество членов ариф. прогрессии
S₃ = ((а+с)/2) *3 = 9
((а+с)/2) *3 = 9
((а+с)/2) = 9/3 =3
(а+с) = 3*2
а+с = 6
определим b - второй член ариф. прогресс.
а+b+с = 9
b = 9-а-с = 9-6 = 3 -второй член ариф. прогресс.
по условию задачи
(а + 1) - первое число геометрической прогрессии
(b + 1) - второе число геометрической прогрессии
(с + 3) - третье число геометрической прогрессии
(а + 1) * (b + 1) * (с + 3) геометр. прогрессия
где b + 1 = 3+1 = 4 второй член геометр. прогрессии
второй член. геом. прогрессии вычисляется по формуле b₂=b₁*q ( где q - знаменатель геом. прогрессии)
следовательно:
b = (а+1) * q
4 = (а+1) * q
q = 4/(а+1)
выразим третий член геом. прогрессии (с + 3) по формуле b₃=b₂*q
(с + 3) = 4*q (подставим в формулу значение q = 4/(а+1))
с+3 = 4*4/(а+1)
с+3 = 16/(а+1)
с = (16/(а+1)) - 3общий знаменатель (а+1)
с = (16-3а-3) / (а+1)
с=(13-3а) / (а+1)
подставим значение с в формулу а+с = 6 (смотри в начале решения)
а + ((13-3а) / (а+1)) = 6 ---левую часть под общий знаменатель (а+1)
(а*(а+1) +13-3а) / (а+1) = 6
а² + а + 13 - 3а = 6*(а+1)
а²-2а+13 = 6а +6
а² - 8а + 7 = 0отсюда находим а = 1 - первый член ариф. прогр.
проверка1²- 8*1 + 7 = 0
т. к. а+с = 6, значит с = 6-а=6-1 = 5 - третий член ариф. прогрессии
итого: а = 1 - первый член ариф. прогр.
b=3 - второй член ариф. прогресс.
с = 5 - третий член ариф. прогрессии
проверка: а+b+с = 1+3+5= 9 -верно
(а + 1)=1+1 = 2 - первое число геометрической прогрессии
(b + 1) =3+1 = 4 - второе число геометрической прогрессии
(с + 3)=5+3 = 8 - третье число геометрической прогрессии
q = 4/(а+1) = 4/(1+1)= 2 -знаменатель геом. прогрессии
проверка: 2*2=44*2=8верно