Случайная величина X распределена по биномиальному закону.
Всего n = 7 испытаний. Вероятность успеха в одном испытании равна p = 0.4, тогда q = 1 - р = 0.6
1) Вероятность того, что стрелок попадет в цель ни разу
2) Вероятность того, что стрелок попадет в цель один раз
3) Вероятность того, что стрелок попадет в цель два раза
4) Вероятность того, что стрелок попадет в цель три раза
5) Вероятность того, что стрелок попадет в цель четыре раза
6) Вероятность того, что стрелок попадет в цель пять раз
7) Вероятность того, что стрелок попадет в цель шесть раз
8) Вероятность того, что стрелок попадет в цель 7 раз
Закон распределения случайной величины X:
а).
Просто подставляем в уравнение, задающее функцию, :
б).
Найдем те значения , при которых значение функции становится равным :
в).
Для того, чтобы определить, принадлежит ли точка графику, подставим в уравнение функции и , и посмотрим, что получится:
Получилось верное равенство! Значит, точка действительно принадлежит графику рассматриваемой функции.
___________________________________________
Задача заключается в решении неравенства :
Получаем, что , или .
Ноли функции - это те значения , при которых :
Значит, единственный ноль функции .
Область определения функции - это те значения , при которых функция существует.
А функция существует только в том случае, если ее знаменатель не равен нолю:
То есть, область определения данной функции - все действительные , кроме :
Задача решена!
Случайная величина X распределена по биномиальному закону.
Всего n = 7 испытаний. Вероятность успеха в одном испытании равна p = 0.4, тогда q = 1 - р = 0.6
1) Вероятность того, что стрелок попадет в цель ни разу
2) Вероятность того, что стрелок попадет в цель один раз
3) Вероятность того, что стрелок попадет в цель два раза
4) Вероятность того, что стрелок попадет в цель три раза
5) Вероятность того, что стрелок попадет в цель четыре раза
6) Вероятность того, что стрелок попадет в цель пять раз
7) Вероятность того, что стрелок попадет в цель шесть раз
8) Вероятность того, что стрелок попадет в цель 7 раз
Закон распределения случайной величины X:
а).
Просто подставляем в уравнение, задающее функцию,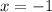 :
:
б).
Найдем те значения , при которых значение функции становится равным
, при которых значение функции становится равным  :
:
в).
Для того, чтобы определить, принадлежит ли точка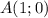 графику, подставим в уравнение функции
графику, подставим в уравнение функции 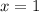 и
и 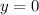 , и посмотрим, что получится:
, и посмотрим, что получится:
Получилось верное равенство! Значит, точка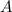 действительно принадлежит графику рассматриваемой функции.
действительно принадлежит графику рассматриваемой функции.
___________________________________________
Задание № 2.а).
Задача заключается в решении неравенства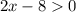 :
:
Получаем, что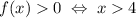 , или
, или 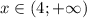 .
.
б).
Ноли функции - это те значения , при которых
, при которых 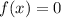 :
:
Значит, единственный ноль функции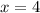 .
.
___________________________________________
Задание № 3.а).
Область определения функции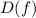 - это те значения
- это те значения  , при которых функция существует.
, при которых функция существует.
А функция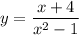 существует только в том случае, если ее знаменатель не равен нолю:
существует только в том случае, если ее знаменатель не равен нолю:
То есть, область определения данной функции - все действительные , кроме
, кроме 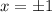 :
:
Задача решена!