Часовая стрелка проходит 5 делений циферблата в час, минутная - 60 делений.
За минуту часовая проходит часть деления, минутная - 1 деление. Значит за 1 минуту минутная стрелка "догоняет" часовую на часть деления.
В настоящий момент стрелки разделяет деления (см. рис. - считаем по часовой стрелке).
Когда минутная стрелка в первый раз поравняется с часовой, ей нужно будет "догнать" часовую ещё 7 раз, сократив расстояние на 60 делений, то есть всего на 60·7 = 420 делений.
делений нужно пройти минутной стрелке, чтобы в восьмой раз поравняться с часовой.
минут понадобится, чтобы минутная стрелка в восьмой раз поравнялась с часовой
Если в пространстве задана точка Мо(хо, уо, zо), то уравнение плоскости, проходящей через точку Мo перпендикулярно вектору нормали (A, B, C) имеет вид: A(x – xо) + B(y – yо) + C(z – zо) = 0.
Так как перпендикуляр, опущен из начала координат на эту плоскость, то нормальный вектор равен MО(−7; 1; 3).
Часовая стрелка проходит 5 делений циферблата в час, минутная - 60 делений.
За минуту часовая проходит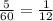 часть деления, минутная - 1 деление. Значит за 1 минуту минутная стрелка "догоняет" часовую на
часть деления, минутная - 1 деление. Значит за 1 минуту минутная стрелка "догоняет" часовую на 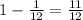 часть деления.
часть деления.
В настоящий момент стрелки разделяет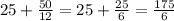 деления (см. рис. - считаем по часовой стрелке).
деления (см. рис. - считаем по часовой стрелке).
Когда минутная стрелка в первый раз поравняется с часовой, ей нужно будет "догнать" часовую ещё 7 раз, сократив расстояние на 60 делений, то есть всего на 60·7 = 420 делений.
Если в пространстве задана точка Мо(хо, уо, zо), то уравнение плоскости, проходящей через точку Мo перпендикулярно вектору нормали (A, B, C) имеет вид: A(x – xо) + B(y – yо) + C(z – zо) = 0.
Так как перпендикуляр, опущен из начала координат на эту плоскость, то нормальный вектор равен MО(−7; 1; 3).
Получаем уравнение -7(x + 7) + (y - 1) + 3)z - 3) = 0.
Раскроем скобки: -7x - 49 + y - 1 + 3z - 9 = 0
-7x + y + 3z = 59 и разделим об части на 59.
(x/(-59/7)) + (y/59) + (z/(59/3)) = 1. Это уравнение в "отрезках".
ответ: длина отрезка, отсекаемого найденной плоскостью от оси OY, равна 59.