Виберіть можливий розклад квадратного тричлена ​

Объяснение:

16. Во сколько раз увеличится объем куба, если его ребра увеличить в два раза?

Решение.

Первоначальный объем куба    V1=a³. (a - длина ребра).

Увеличим  ребро в 2 раза. стало 2а

При этом объем стал V2=(2a)³=2³*a³=8a².

V2/v1=8a³/a³=8 раз.

ответ:  4) 8.

----------------------

17. В треугольнике ABC, AC = ВС = 365, AB = 24 . Найдите tg А.

Проведем высоту СН. Так как треугольник равнобедренный, то АН=ВН=24/2=12.

TgA=CH/AH - отношение противолежащего катета к прилежащему.

По т. Пифагора СН=√(АС²-АН²)=√(365²-12²)=364.8

tgA=364.8/12=30.4.    нет правильного ответа.

-------------------

18. Найдите значение коэффициента k, при котором кривая

у = х² + kx +4 касается оси Ох;

ответ  +4.  (См. скриншот)

(см. объяснение)

Объяснение:

Берем первую производную:

По условию нужно, чтобы имелся строгий экстремум.

Тогда берем вторую производную:

Перейдем к системе, чтобы с ее найти значения параметра, которые нужно исключить:

Система не имеет решений.

Вернемся к первой производной:

В таких случаях выгодно строить схематичную параболу, описывая каждое интересующее нас расположение на языке математики.

Учитывая, что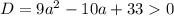  , получим:

(см. прикрпепленный файл)

Запишем систему:

То есть нужно решить:

Итого при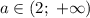 точки экстремума функции принадлежат промежутку .

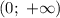Задание выполнено!