Виберіть правильно записаний розклад на лінійні множники деякого квадратного тричлена, якщо a = 1, x1 = -3, x2 = 5.
(х+3)(х + 5)
(х – 3) (x+5)
(х - 3)(х – 5)
(х+3)(х – 5)
Інше:​

3

Объяснение:

остання цифра добутку (степені числа) залежить лише від добутку останньої цифри кожного з множників

тому  остання цифра числа 987 в степені 987 така ж сама як і остання цифра числа 7 в степені 987

далі 7 =..7 (1 раз множник)

7*7=...9 (2 рази множник)  

7*7*7=..3 ( 3 рази множник)

7*7*7*7=..1 ( 4 рази множник)

7*7*7*7*7=..7 ( 5 раз множник), а значить остання цифра степеней 7 буде повторюватися з періодом 4

987=4*246+3

7 в степені 987=7*7*7**7*7 (987 раз)=

(7*7*7*7) (246 раз) *7*7*7=(...1)(246 раз)*...3=...1*..3=...3

значить остання цифра 3

Здравствуйте, Sonya2006f!

Чтобы восстановить неполный квадрат суммы, нужно представить крайние члены данной формулы в виде числа со степенью.

Разложение чисел на простые множители:

Теперь когда мы знаем, как представить данные члены в виде числа со степенью, запишем формулу, по которой выполнялось разложение.

Формула сокращённого умножения:

НЕПОЛНЫЙ КВАДРАТ СУММЫ:  .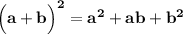

Зная, что первоначально выражение имело вид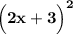   , перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.

Разложение данного выражения на множители:

Окончательный ответ данной задачи:

Неполный квадрат суммы данного выражения - "6x".

С Уважением, NeNs07.