Скрорость теплохода примем за x(км/час), а скорость течения - за y(км/час). Тогда скорость теплохода по течению будет (x+y)(км/час), а скорость теплохода против течения (x-y)(км/час). Расстояние равняется произведению скорости на время, следовательно, можем составить систему уравнений: В первом уравнении раскрываем скобки, второе же уравнение умножаем на 2: Из второго уравнения выражаем y и подставляем в первое: Далее, решаем первое уравнение относительно x: Таким образом, собственная скорость теплохода равняется 55 км/час, а скорость течения - 5 км/час. Можно сделать проверку, подставив найденные скорости в изначальные уравнения.
ответ: 1-б. 2-а, 3-г, 4-, 5- , 6-в, 7-г
Объяснение:
1. Найдите значение алгебраической дроби 2х/х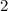
-1, при х= 1/3
• а) 0,75; б) -0,75 ; в) - ;г) -1,5
2. Найдите значение x, при котором дробь х+2/х-4 не имеет смысла
а)4 б)-2 в) -4 г) нет таких значений
3. Какое из предложенных выражений записано в виде алгебраической дроби?
а)2х/3+х ; б)2/х2+3х в)81х2/13-х ; г)2/3-х
4. Найдите значение выражения , при а= -0,7, в=0,3
а)2,5; б) -2,5; в) 1; г) другой ответ.
5.При каком значении а дробь не определена?
а) 0; б) - ; в) ; г)другой ответ.
6. Найди допустимые значения букв, входящих в дробь а/b
а) любые значения; б)5 возможных значений ; в) любые значения а и b, при b не равным 0 ; г) нет ответа
7.Выберите дробно- рациональные выражения 2х/3+4/7, 2-5х/7,3, 3/х-2
а) нет правильного ответа ; б) 2х/3+4/7 ; в)2-5х/7,3 ; г) 3/х-2
В первом уравнении раскрываем скобки, второе же уравнение умножаем на 2:
Из второго уравнения выражаем y и подставляем в первое:
Далее, решаем первое уравнение относительно x:
Таким образом, собственная скорость теплохода равняется 55 км/час, а скорость течения - 5 км/час. Можно сделать проверку, подставив найденные скорости в изначальные уравнения.