Визначити знак виразу ctg 250× sin 130​

Решить систему уравнений графически - построить графики всех уравнений в одной системе координат, найти их точки пересечения и выписать в ответ.

1-я функция - квадратичная, график - парабола, самая стандартная.

2-я функция - линейная, прямая пропорциональность, самая простенькая прямая, которая является биссектрисой угла первой координатной четверти (да и третьей тоже).

Графики с табличками приложены (для прямой избыточно, ведь для её построения достаточно 2 точки)

Получили 2 точки пересечения

ответ: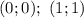

9/x² + 9/(x + 2)² = 10

x ≠ 0  x ≠ -2

замена x = y-1

9/(y - 1)² + 9/(y + 1)² = 10

9*((y - 1)² + (y + 1)²) = 10*(y - 1)²(y + 1)²

9(y² - 2y + 1 + y² + 2y + 1) = 10(y² - 1)²

9(2y² + 2) = 10(y² - 1)²

9*2(y² + 1) = 10(y² - 1)²

9(y² + 1) = 5(y² - 1)²

y² = t >=0 (если брать только действительные корни)

9t + 9 = 5t² - 10t + 5

5t² - 19t - 4 = 0

D = 19² + 80 = 21²

t12= (19 +- 21)/10 = 4   -1/5

t1=-1/5 нет действительных корней (если есть комплексные то y=+-i√1/5  x = -1 +- i√1/5))

t2 = 4

y² = 4

y1 = 2   x1 = y - 1 = 1

y1 = -2  x2= y - 1 = -3

ответ x = {-1, -3} (если нужны комплексные то x = -1 +- i√1/5)