Визначте чи паралельні прямі а і в, якщо кут 1=36°, а кут 2 в 4 рази менший ніж кут 3. ​

y= x² - 4x +3  . Это парабола ,ветви вверх. Область определения :х-любое, множество значений функции [ -1; +∞) ;

a)  найдите точки пересечения графика с осью ОУ

Точки пересечения с оу ( х=0)

у= 0²- 4*0+3= 3, Точка (0; 3).

b)  найдите точки пересечения графика с осью ОХ;

Точки пересечения с осью ох( у=0)

x²- 4x+3=0 , Д=4 , х₁=(4+2)/2=3,   х₂=(4-2)/2=1  . Точки (3;0) , ( 1;0);

c)  запишите координаты вершины параболы

х₀=-в/2а,   х₀=-(-4)/2= 2 ,  у₀=2²-4*2 +3= -1 , ( 2;  -1).  

Тогда наименьшее значение функции у=-1 ( при х=2)

Наибольшего значения нет    ;

d)  запишите уравнение оси симметрии параболы

х=2;

Дополнительно

f) Промежутки возрастания убывания функции

Функция убывает при х≤ 2 ,

функция возрастает при  x≥2;

Промежутки знакопостоянства функции :

 +                  . -                .+

______(1)_______(3)_______

у>0 при    х <1 и x>3

у<0 при  1 <х< 3 ;

а)

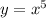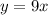Рассмотрим две функции: и . Обе эти функции возрастающие. Тогда и функция, представляющая сумму эти[ функций, то есть функция 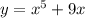будет возрастающей.

Таким образом, в левой части стоит возрастающая функция. Но возрастающая функция принимает каждое свое значение в единственной точке. Это означает, что если найден некоторый корень заданного уравнения, то других корней у уравнения нет.

Корень угадывается достаточно легко: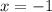 . Проверка:

ответ: -1

б)

Аналогично, каждая из функци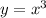й и 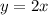возрастает. Значит, возрастает и функция .

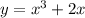Таким образом, уравнение имеет не более одного корня. Этот корень также легко подбирается: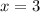 . Проверка:

ответ: 3