Водолазный колокол, содержащий в начальный момент времени v=2 моля воздуха объeмом V1=112 л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeмa V2 . Работа, совершаемая водой при сжатии воздуха, определяется выражением A=Альфа*v*Tlog2V1/V2 (Дж), где(альфа=5.75) постоянная, а Т=300К — температура воздуха. Какой объeмV2 (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 17250 Дж?
Пусть скорость третьего велосипедиста равна v км/ч,
а t ч - время, за которое он догнал второго велосипедиста.
До встречи третий и второй велосипедисты проехали одно и то же расстояние.
По условию задачи, второй ехал на 1 час больше, чем третий.
Тогда t+1 ч - время второго
Получаем:
Скорость (км/ч) Время (ч) Расстояние (км)
третий v t v*t
второй 21 t+1 21*(t+1)
Составляем первое уравнение: vt=21(t+1)
До встречи первый и третий проехали одинаковое расстояние, третий догнал первого через t+9 часов,
а первый на тот момент уже был в пути t+2+9=t+11 часов, т.к. выехал на 2 часа раньше третьего.
Получаем:
Скорость (км/ч) Время (ч) Расстояние (км)
третий v t+9 v*(t+9)
второй 24 t+11 24*(t+11)
Составляем второе уравнение: v(t+9)=24(t+11)
Решаем систему уравнений:
{ vt=21(t+1) => v=21(t+1)/t (подставим во второе уравнение)
{ v(t+9)=24(t+11)
Итак, t=3 часа
Находим скорость третьего велосипедиста:
ответ: 28 км/ч
а - длина прямоугольника
b - ширина прямоугольника
а - ? см, на 4 см >, чем b
b - ? см
S=60 см²
Р - ? см
подставим известные величины
перенесём всё в левую часть и приравняем уравнение к нулю, при этом не забываем сменить знак на противоположный
Квадратное уравнение имеет вид: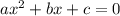
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
не удовлетворяет условию задачи, так как сторона прямоугольника не может быть отрицательной
следовательно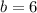
(см) - ширина прямоугольника.
ответ: 32 см периметр прямоугольника.