1) Очень дико видеть "область определения", потому что это то, что задаёт математик. Область существования вещественных прообразов называть "область определения" — дичь! Так вот, область существования аргумента здесь — всё множество действительных чисел ("вся числовая прямая").
2) Пересечение с осью аргументов означает равенство . То есть требуется решить уравнение . Это алгебраическое уравнение второго порядка. Два его корня суть 6 и -2.
3) Чётность/нечётность относительно оси значений (x = 0)? Нет, не обладает свойствами ни чётности, ни нечётности.
4) Тут меня раза три остановили, когда я стал исследовать на экстремумы через производную. Если исследовать всё-таки через производные, то
Точки экстремума: 0[/tex]
Вторая производная: => выпуклость вверх для любого значения агрумента (прообраза) => точки экстремума — максимумы.
Функция монотонно возрастает при x < 1 и монотонно убывает при x > 1.
5) Точки экстремумов были найдены выше.
6) Рисунок 1 в аттаче.
7) Они хотят интеграл? Ого. Не, это только завтра.
Рассмотрим по порядку: 1. Похоже, потерялся знак >, потому что стоит точка. Тогда неравенство верно, ведь если из большего числа отнять меньшее, то получится положительное число, а оно явно больше -21. 2. Неверно, так как чем больше абсолютная величина отрицательного числа, тем это число меньше. Например, пусть a = 10, b = 5 (нам разрешено брать натуральные a и b). Тогда -2*10 < -2*5, потому что -20 < -10 3. Неверно, потому что частное меньше единицы, если числитель меньше знаменателя, а по условию a > b 4. Неверно, ибо a > b
Функция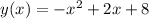
1) Очень дико видеть "область определения", потому что это то, что задаёт математик. Область существования вещественных прообразов называть "область определения" — дичь! Так вот, область существования аргумента здесь — всё множество действительных чисел ("вся числовая прямая").
2) Пересечение с осью аргументов означает равенство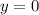 . То есть требуется решить уравнение
. То есть требуется решить уравнение 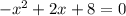 . Это алгебраическое уравнение второго порядка. Два его корня суть 6 и -2.
. Это алгебраическое уравнение второго порядка. Два его корня суть 6 и -2.
3) Чётность/нечётность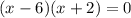 относительно оси значений (x = 0)? Нет, не обладает свойствами ни чётности, ни нечётности.
относительно оси значений (x = 0)? Нет, не обладает свойствами ни чётности, ни нечётности.
4) Тут меня раза три остановили, когда я стал исследовать на экстремумы через производную. Если исследовать всё-таки через производные, то
Точки экстремума: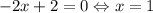 0[/tex]
0[/tex]
Вторая производная: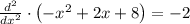 => выпуклость вверх для любого значения агрумента (прообраза) => точки экстремума — максимумы.
=> выпуклость вверх для любого значения агрумента (прообраза) => точки экстремума — максимумы.
Функция монотонно возрастает при x < 1 и монотонно убывает при x > 1.
5) Точки экстремумов были найдены выше.
6) Рисунок 1 в аттаче.
7) Они хотят интеграл? Ого. Не, это только завтра.
1. Похоже, потерялся знак >, потому что стоит точка. Тогда неравенство верно, ведь если из большего числа отнять меньшее, то получится положительное число, а оно явно больше -21.
2. Неверно, так как чем больше абсолютная величина отрицательного числа, тем это число меньше. Например, пусть a = 10, b = 5 (нам разрешено брать натуральные a и b). Тогда -2*10 < -2*5, потому что -20 < -10
3. Неверно, потому что частное меньше единицы, если числитель меньше знаменателя, а по условию a > b
4. Неверно, ибо a > b