Вскобках (числитель): 3 корня из 5 за скобкой вторая степень поделить на 15

Выразить, например из первого уравнения х и подставить во второе:


Подставляем:

Теперь полученный y подставляем сюда чтобы найти х

ответ получается: (6; -1)

Можно еще другим сложением/вычитанием одного уравнения из другого.
Сложение:

Складываются иксы с иксами, игреки с игреками и числа с числами, т.е. (x+x)=2x, (y+(-y)=y-y=0) и (5+7=12)
И получается в результате сложения одно уравнение с оной неизвестной:

Полученный х подставляем в любое уравнение:


ответ получается такой же: (6; -1)

Или вычитанием, тут тоже самое что и в сложении, только соответственно вместо сложения выполняется вычитания, также иксов из иксов, игреков из игреков и чисел с чисел, т.е. (x-x)=0, (y-(-y)=y+y=2y) и (5-7=-2)
И получается в результате вычитания одно уравнение с оной неизвестной:

Полученный y подставляем в любое уравнение:


ответ получается снова такой же: (6; -1)

Відповідь:

Пояснення:

Перетворимо рівняння системи. Обидві частини першого рівняння системи помножимо на 10, а друге - на 12, отримаємо наступну систему рівняння: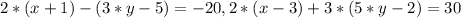

Розкриємо дужки:

Зведемо подібні доданки в лівих частинах обох рівнянь системи, отримаємо:

Значення зі змінної залишаємо в лівій частині, а вільні числа переносимо до правої частини, змінюючи знак на протилежний:

Виконуємо алгебраїчні обчислення в правих частинах обох рівнянь системи:

Помножимо обидві частини першого рівняння на 5, отримаємо рівняння:

Використовуючи метод додавання, додамо обидві рівняння системи між собою, отримаємо:

Знаходимо змінну :

Підставимо змінну у будь-яке рівняння системи та знайдемо змінну 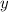, отримаємо: