x² + px + q = 0 сумма корней равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
x₁ + x₂= -p
x₁ · x₂= q
14 + x₂ = 26
x₂=26-14=12
q=14*12=168
x²-26x+168=0 - при желании можно проверить, подставив в уравнение корни, можно для проверки решить через дискриминант.
144-312+168=0
задача
70 м; 110 м
Периметр прямоугольника со сторонами а и b: Р = 2 * (a + b).
Площадь прямоугольника: S = a * b.
Следовательно, получим систему уравнений:
2 * (a + b) = 360.
a * b = 7700.
Решаешь системой уравнений
(a + b) =230
a=7700/b
7700/b+b=230
b^2 – 230 * b + 7700=0
6
Объяснение:
В голову приходит только тупое громоздкое решение.
Допустим в прогрессии n членов
первый член b₁
второй b₂=b₁q
предпоследний bₙ₋₁=b₁qⁿ⁻²
последний bₙ=b₁qⁿ⁻¹
Получаем систему из трех уравнений
b₁+b₁qⁿ⁻¹=66
b₁q*b₁qⁿ⁻²=128
Решаем
b₁²qⁿ⁻¹=128
из второг уравнения получаем qⁿ⁻¹=128/b₁² и подставляем в первое
b₁+128/b₁=66
b₁²-66b₁+128=0
D=66²-4*128=(2*33)²-4*128=4(33²-128)=4*(1089-128)=4*961=2²*31²
√D=2*31
b₁=(66±2*31)/2=33±31
Два возможных значения b₁; 2 и 64
1) b₁=2
qⁿ⁻¹=128/4=32
запишем третье уравнение в виде и подставим в него значения b₁ и qⁿ⁻¹
1-32q=63-63q
31q=62
q=2
2ⁿ⁻¹=32
2ⁿ⁻¹=2⁵
n-1=5
n=6
2) b₁=64
qⁿ⁻¹=128/64²=1/32
и подставим в третье уравнения значения b₁ и qⁿ⁻¹
32-q=63-63q
62q=31
2ⁿ⁻¹=1/32
2ⁿ⁻¹=2⁻⁵
n-1=-5
n=-4 посторонний корень.
x² + px + q = 0 сумма корней равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
x₁ + x₂= -p
x₁ · x₂= q
14 + x₂ = 26
x₂=26-14=12
q=14*12=168
x²-26x+168=0 - при желании можно проверить, подставив в уравнение корни, можно для проверки решить через дискриминант.
144-312+168=0
задача
70 м; 110 м
Периметр прямоугольника со сторонами а и b: Р = 2 * (a + b).
Площадь прямоугольника: S = a * b.
Следовательно, получим систему уравнений:
2 * (a + b) = 360.
a * b = 7700.
Решаешь системой уравнений
(a + b) =230
a=7700/b
7700/b+b=230
b^2 – 230 * b + 7700=0
6
Объяснение:
В голову приходит только тупое громоздкое решение.
Допустим в прогрессии n членов
первый член b₁
второй b₂=b₁q
предпоследний bₙ₋₁=b₁qⁿ⁻²
последний bₙ=b₁qⁿ⁻¹
Получаем систему из трех уравнений
b₁+b₁qⁿ⁻¹=66
b₁q*b₁qⁿ⁻²=128
Решаем
b₁+b₁qⁿ⁻¹=66
b₁²qⁿ⁻¹=128
из второг уравнения получаем qⁿ⁻¹=128/b₁² и подставляем в первое
b₁+128/b₁=66
b₁²-66b₁+128=0
D=66²-4*128=(2*33)²-4*128=4(33²-128)=4*(1089-128)=4*961=2²*31²
√D=2*31
b₁=(66±2*31)/2=33±31
Два возможных значения b₁; 2 и 64
1) b₁=2
qⁿ⁻¹=128/4=32
запишем третье уравнение в виде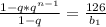
и подставим в него значения b₁ и qⁿ⁻¹
1-32q=63-63q
31q=62
q=2
2ⁿ⁻¹=32
2ⁿ⁻¹=2⁵
n-1=5
n=6
2) b₁=64
qⁿ⁻¹=128/64²=1/32
и подставим в третье уравнения значения b₁ и qⁿ⁻¹
32-q=63-63q
62q=31
q=2
2ⁿ⁻¹=1/32
2ⁿ⁻¹=2⁻⁵
n-1=-5
n=-4 посторонний корень.