Можно заметить, что если от любого элемента множества А отнять 1, то получится элемент множества B.
Тогда, если x - четное натуральное число, y - нечетное натуральное число, то:
б)
Множество квадратов натуральных чисел:
Множество кубов натуральных чисел:
Можно заметить, что если из любого элемента множества C извлечь квадратный корень и получившееся число возвести в куб, то получится элемент множества D.
Тогда, если x - квадрат натурального числа, y - куб натурального числа, то:
{6x-5y=43 {x=(43+5y)/6 {x=(43+5y)/6 {x=(43+5y)/6
{4x+3y=73 {4*(43+5y)/6+3y=73 {(86+10y)+9y=219 {19y=133
{x=(43+5y)/6 {x=(43+35)/6=78/6=13
{y=7 {y=7
ответ: x=13
y=7
{5x+10y=54 {x=(54-10y)/5 {x=10.8-2y {x=10.8-2y
{10x+5y=46,5 {10x+5y=46,5 {10(10.8-2y)+5y=46,5 {108+(-20+5)y=46,5
{x=10.8-2y {x=10.8-2y {x=10.8-8.2=2.6
{15y=61.5 {y=4.1 {y=4.1
ответ: x=2.6
y=4.1
{12x-7y=2 {7y=12x-2 {y=(12x-2)/7 {y=(12x-2)/7
{9x+14y=7 {9x+14y=7 {9x+14*(12x-2)/7=7 {9x+24x-4=7
{y=(12x-2)/7 {y=(12x-2)/7 {y=(12/3-2)/7 {y=(4-2)/7 {y=2/7
{33x=11 {x=1/3 {x=1/3 {x=1/3 {x=1/3
ответ: x=1/3
y=2/7
а)
Множество четных натуральных чисел: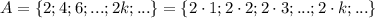
Множество нечетных натуральных чисел: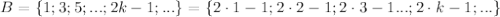
Можно заметить, что если от любого элемента множества А отнять 1, то получится элемент множества B.
Тогда, если x - четное натуральное число, y - нечетное натуральное число, то:
б)
Множество квадратов натуральных чисел: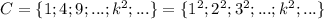
Множество кубов натуральных чисел: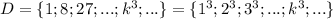
Можно заметить, что если из любого элемента множества C извлечь квадратный корень и получившееся число возвести в куб, то получится элемент множества D.
Тогда, если x - квадрат натурального числа, y - куб натурального числа, то: