№1
а) (x-4)^2=x^2-8x+16
б) (3x-5)^2=9x-30x=25
в) (2a-3)*(2a+3)=4a^2-9
г) (y^2-2)*(y^2+2)=y^4-4
№2
а) b^2-0.36=(b-0.6)*(b+0.6)
б) y^2-6y+9=(y-3)^2
№3
(2a-3b)*3b+(a-3b)^2
a=
Упрощаем выражение:
6ab-9b^2+a^2-6ab+9b^2
Сокращаем все что сокращается:
a^2
Теперь решаем:
ответ:
№4
а) 5(2-3xy)(2+3xy)=20-45x^2y^2
б) (a^3-b^2)^2=a^6-2*a^3*b^2+b^4
в) (x+y)^2-(x-y)^2=4xy
№5
(6a-1)(6a+1)-4a(9a+2)=-1
-1-8a=-1
Данное уравнение не решаемо.
№6
(2x+3)(3x-7)-(x+1)(x-1)
6x^2-5x-21-x^2+1
Снова упрощаем выражение:
5x^2-5x-20
Проверяем правильность утверждения что это выражение делится на 5 при любом целом "x"
Пусть x=8
Значит выражение теперь выглядит так:
(5*8)^2-5*8-20
Решать дальше смысла нет, так как при любом целом "x" последней цифрой будет ноль, значит выражение будет делится на 5.
Исключение это "x=1" в результате выражение будет равно 1.
Если это учесть то утверждение неверно!
Удачи, надеюсь
Смотри в решении
Объяснение:
Вариант 1
Всегда будем избавляться от знаменателей путем домножения на наименьший общий знаменатель во всех заданиях
5.
а. 3x<5
x<1 ⅔
б. х>0×8
х>0
в. 4х>=6
х>=1 ⅔
г. 5х<=0
х<=0
6.
а. 2+х<20
х<18
б. 3-х>18
х<-15
в. 1+6х<=7
6х<=6
х<=1
г. 7-2х>=0
2х<=7
Х<=3 ½
Вариант 2.
1.
а. 5х>2
х> 0,4
б. х<0×4
х<0
в. 2х>=27
х>=13,5
г. 4х<=0
2.
а. 5+3х<2
3х<-3
х<-1
б. 4-х>=0
х<=4
в. 1-х<20
х>-19
г. 2+5х>=0
5х>=-2
х>=-0,4
№1
а) (x-4)^2=x^2-8x+16
б) (3x-5)^2=9x-30x=25
в) (2a-3)*(2a+3)=4a^2-9
г) (y^2-2)*(y^2+2)=y^4-4
№2
а) b^2-0.36=(b-0.6)*(b+0.6)
б) y^2-6y+9=(y-3)^2
№3
(2a-3b)*3b+(a-3b)^2
a=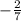
Упрощаем выражение:
6ab-9b^2+a^2-6ab+9b^2
Сокращаем все что сокращается:
a^2
Теперь решаем:
ответ: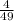
№4
а) 5(2-3xy)(2+3xy)=20-45x^2y^2
б) (a^3-b^2)^2=a^6-2*a^3*b^2+b^4
в) (x+y)^2-(x-y)^2=4xy
№5
(6a-1)(6a+1)-4a(9a+2)=-1
Упрощаем выражение:
-1-8a=-1
Данное уравнение не решаемо.
№6
(2x+3)(3x-7)-(x+1)(x-1)
Упрощаем выражение:
6x^2-5x-21-x^2+1
Снова упрощаем выражение:
5x^2-5x-20
Проверяем правильность утверждения что это выражение делится на 5 при любом целом "x"
Пусть x=8
Значит выражение теперь выглядит так:
(5*8)^2-5*8-20
Решать дальше смысла нет, так как при любом целом "x" последней цифрой будет ноль, значит выражение будет делится на 5.
Исключение это "x=1" в результате выражение будет равно 1.
Если это учесть то утверждение неверно!
Удачи, надеюсь
Смотри в решении
Объяснение:
Вариант 1
Всегда будем избавляться от знаменателей путем домножения на наименьший общий знаменатель во всех заданиях
5.
а. 3x<5
x<1 ⅔
б. х>0×8
х>0
в. 4х>=6
х>=1 ⅔
г. 5х<=0
х<=0
6.
а. 2+х<20
х<18
б. 3-х>18
х<-15
в. 1+6х<=7
6х<=6
х<=1
г. 7-2х>=0
2х<=7
Х<=3 ½
Вариант 2.
1.
а. 5х>2
х> 0,4
б. х<0×4
х<0
в. 2х>=27
х>=13,5
г. 4х<=0
х<=0
2.
а. 5+3х<2
3х<-3
х<-1
б. 4-х>=0
х<=4
в. 1-х<20
х>-19
г. 2+5х>=0
5х>=-2
х>=-0,4