Вычисли, в каких границах заключено число p=3,16+-0,02.
Укажи ответ в виде двойного неравенства:
←=р←=​

1) 1-я бригада выполняет задание за 40 дней, 2-я бригада - за 10 дней

2) 1-я бригада выполняет задание за 12 дней, 2-я бригада - за 24 дня.

Объяснение:

Пусть С - объём производственного задания

х - время, за которое задание выполняет 1-я бригада

- производительность 1-й бригады

у - время за которое задание выполняет 2-я бригада

- производительность 2-й бригады

- производительность бригад при совместной работе

- время выполнения задания при совместной работе

По условию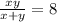         (1)

- время выполнения 1-й бригадой 1/3 задания

- время выполнения 2-й бригадой оставшихся 2/3 задания

По условию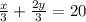   ⇒ x + 2y = 60  ⇒ x = 60 - 2y   (2)

Подставим (2) уравнение в (1)

60y - 2y² = 480 - 8y

2y² - 68y + 480

y² - 34y + 240 = 0

D = 34² - 4 · 240 = 196

√D = 14

y₁ = 0.5(34 - 14) = 10 (дней)     х₁ = 60 - 2 · 10 = 40 (дней)      

у₂ = 0,5(34 + 14) = 24 (дня)     х₂ = 60 - 2 · 24 = 12 (дней)

1)Можно вынести общего множителя за скобки.
Используем распределительный закон ac + bc = c(a + b)Например - 12 y ^3 – 20 y ^2 = 4 y ^2 · 3 y – 4 y ^2 · 5 = 4 y ^2 (3 y – 5). 
2)Использовать формулу сокращенного умножения.
x ^4 – 1 = ( x ^2 )^ 2 – 1 ^2 = ( x^ 2 – 1)( x^ 2 + 1) = ( x ^2 – 1 ^2 )( x ^2 + 1) = ( x + 1)( x – 1)( x 2 + 1). 
группировки
x^3 – 3 x 2 y – 4 xy + 12 y ^2 = ( x ^3 – 3 x 2 y ) – (4 xy – 12 y ^2 ). 
В первой группе мы вынесли за скобку общий множитель x^2, а во второй − 4y . В результате получаем: 
( x ^3 – 3 x 2 y ) – (4 xy – 12 y ^2 ) = x 62 ( x – 3 y ) – 4 y ( x – 3 y ). 
Теперь общий множитель ( x – 3 y ) можем вынести за скобки: 
x ^2 ( x – 3 y ) – 4 y ( x – 3 y ) = ( x – 3 y )( x^2 – 4 y ).