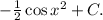Обозначим данный интеграл буквой I.
Обратим внимание на конструкцию
Тогда интеграл примет вид:
Теперь для удобства заменим x² = t:
Вернемся к переменной х:
ответ:
Обозначим данный интеграл буквой I.
Обратим внимание на конструкцию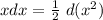
Тогда интеграл примет вид:
Теперь для удобства заменим x² = t:
Вернемся к переменной х:
ответ: