Вычислить интегралл 2сверхуSснизу1 1/3dx (еще на фото)

1)

Так как значения синуса не могут быть большими единицы, получаем:

Так как выражение под радикалом и собственно весь радикал не могут быть отрицательными получаем:

Откуда получаем:

Объединяя полученные результаты получаем: a∈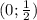

ответ: a∈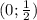

2)

Получаем квадратное уравнение относительно t:

Исходя из того что данное уравнение должно иметь лишь одно решение получаем, что дискриминант должен быть равен нулю:

Но так как нам нужно только одно решение в заданном промежутке получаем:

неравенство не имеет решений

Получаем, что при a∈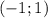 данное уравнение имеет лишь один корень

ответ: a∈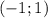

(2+√5) = 1/8 + 3√5/8 + 15/8 + 5√5/8 = (1/2 + √5/2)³ = (1 + √5)³/8

(2 - √5) = 1/8 - 3√5/8 +15/8 - 5√5/5 = (1/2 - √5/2)³ = (1 - √5)³/ 8

∛(2 + √5) + ∛(2 - √5) = ∛(1 + √5)³/2³ + ∛(1 - √5)³/2³ = (1 + √5)/2 + (1 - √5)/2 = 1/2 - √5/2 + 1/2 + √5/2 = 1

ответ   ОДИН

сделаем по другому

a = 2 + √5

b = 2 - √5

∛(2 + √5) + ∛(2 -√5) = c

∛(a*b) = ∛((2 + √5)(2 - √5)) = ∛(-1) = -1 (формула 1)

a + b = 2 + √5 + 2 - √5 = 4 (формула 2)

∛a + ∛b = c  

∛a = c - ∛b (возводим в куб) (формула 3)

a = c³ - 3c²∛b + 3c∛b² - b

c³ = a + 3c²∛b - 3c∛b² + b = a + b + 3c∛b(c - ∛b) ={ по формуле 2 и 3} = 4 + 3c∛b*∛a = {формула 1} =4 - 3c

c³ + 3c - 4 = 0

c³ + c² + 4c - c² - c - 4 = 0

c²(c - 1) + c(c -1) + 4(c-1) = 0

(c - 1)(c² + c + 4) = 0

вспоминаем что ∛(2 + √5) + ∛(2 -√5) = c

первая скобка c = 1

вторая скобка c² + c + 4 = 0 D=1 - 4*4 = -15 дискриминант отрицательный, действительных решений нет (2 комплексных)

ответ 1