Положим . Модуль комплексного числа: ,тогда
По формуле Муавра
Аналогично, положим , тогда , тогда
Тогда по формуле Муавра
Окончательно получаем
Положим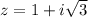 . Модуль комплексного числа:
. Модуль комплексного числа: 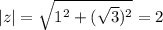 ,тогда
,тогда 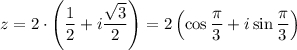
По формуле Муавра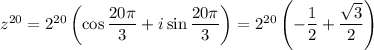
Аналогично, положим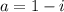 , тогда
, тогда 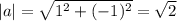 , тогда
, тогда 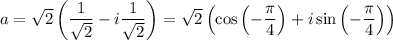
Тогда по формуле Муавра
Окончательно получаем