А теперь подумаем, что будет при взятии целой части числа.
Вот, допустим, f(x)=1 без взятия целой части, при , тогда при любом , но при взятии целой части будет 1. Далее, при некотором , f(x)=2.
Но при любом
При идет прямая, в точка не выколота, а вот в где f(x)=1 выколота, а вот где f(x)=2 не выколота.
И так далее.
При f(x)<0 все симметрично наоборот
На рисунке я постарался отметить все, что нужно. Синяя прямая - исходная прямая графика y=2x+3.4, а вот черные кусочки - нужный график вместо с выколотыми точками.
Пунктирами, по факту, отмечены разрывы функции. Это перпендикуляры к кусочкам графика
Сначала построим график f(x)=2x+3.4
А теперь подумаем, что будет при взятии целой части числа.
Вот, допустим, f(x)=1 без взятия целой части, при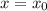 , тогда при любом
, тогда при любом 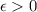
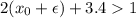 , но при взятии целой части будет 1. Далее, при некотором
, но при взятии целой части будет 1. Далее, при некотором 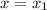 , f(x)=2.
, f(x)=2.
Но при любом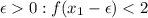
При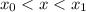 идет прямая, в
идет прямая, в 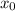 точка не выколота, а вот в
точка не выколота, а вот в 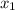 где f(x)=1 выколота, а вот где f(x)=2 не выколота.
где f(x)=1 выколота, а вот где f(x)=2 не выколота.
И так далее.
При f(x)<0 все симметрично наоборот
На рисунке я постарался отметить все, что нужно. Синяя прямая - исходная прямая графика y=2x+3.4, а вот черные кусочки - нужный график вместо с выколотыми точками.
Пунктирами, по факту, отмечены разрывы функции. Это перпендикуляры к кусочкам графика
сos(x - π/6) = cosx ⇔ cos(x -π/6) - cosx = 0 ⇔
-2sin( x - π/6 - x )/2 *sin( x -π/6 +x)/2=0 ⇔ 2sinπ/12 *sin( x - π/12)= 0⇔
sin( x - π/12)= 0 ( т.к. sinπ/12 = √((1 - cosπ/6) / 2)=(1/2)*√(2 - √3) ≠ 0 ) .
x - π/12 = π*n , n∈ Z ;
x = π/12 + π*n , n∈ Z. ( общее решение уравнения )
x ∈ [ - π ; 7π/6 ] , если n = -1 , 0 , 1→ три корней на [ - π ; 7π/6 ]
ответ : три корней {- 11 π /12 ; π/12 ; 13 π /12 }
* * * * * * *
- π ≤ π/12 + π*n ≤ 7π/6 ⇔ - 1 ≤ 1/12 + n ≤ 7/6⇔ -1 -1/12 ≤ n ≤ 7/6 -1/12⇔
-13/12 ≤ n ≤ 13/12 ⇒ n = -1 , 0 , 1
* * * * * * *