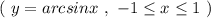logo
Войти Регистрация Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
lyskoyana39
lyskoyana39
04.11.2020 22:51 •  Алгебра

Вычислить определенные интегралы. а)Используя основные свойства и формулы
б )методом подстановки
с)методом интегрированием по частям
​


Вычислить определенные интегралы. а)Используя основные свойства и формулы б )методом подстановки с)

Показать ответ
Ответ:
gejdanp0dmbe
gejdanp0dmbe
01.04.2021 13:11

\int\limits^4_1\, \dfrac{3+\sqrt{x^2}-2x}{\sqrt{4-x^2}}\, dx=\Big[\ \sqrt{x^2}=|x|=x\ ,\ 1\leq x\leq 4\ \Big]=\int\limits^4_1\, \dfrac{3+x-2x}{\sqrt{4-x^2}}\, dx=\\\\\\=3\int\limits^4_1\, \dfrac{dx}{\sqrt{4-x^2}}-\int\limits^4_1\, \dfrac{x\, dx}{\sqrt{4-x^2}}=3\cdot arcsin\dfrac{x}{2}\ \Big|_1^4+\dfrac{1}{2}\int\limits^4_1\, \dfrac{-2x\, dx}{\sqrt{4-x^2}}=\\\\\\=3\cdot (arcsin2-arcsin\dfrac{1}{2})+\dfrac{1}{2}\cdot 2\cdot \sqrt{4-x^2}\ \Big|_1^4=\ ?

Вычислить определённый интеграл невозможно, так как не существует  arcsin2  (\ y=arcsinx\ ,\ -1\leq x\leq 1\ )  

2)\ \ \int\limits^{\pi /4}_0\, x\cdot sin2x\, dx=\Big[u=x\ ,\ du=dx\ ,\ dv=sin2x\, dx\ ,\ v=-\dfrac{1}{2}\, cos2x\ \Big]=\\\\\\=-\dfrac{1}{2}\, x\, cos2x\Big|_0^{\pi /4}+\dfrac{1}{2}\int\limits^{\pi /4}_0\, cos2x\, dx=-\dfrac{1}{2}\cdot 0+\dfrac{1}{4}\cdot sin2x\Big|_0^{\pi /4}=\dfrac{1}{4}\cdot (1-0)=\dfrac{1}{4}

0,0(0 оценок)
Популярные вопросы: Алгебра
zaharovdv73
zaharovdv73
08.11.2022 04:14
-2(3,5у-2,5)+4,5у-1, при у=4...
Aelly
Aelly
20.05.2023 19:29
3y-(y-19)=29, и 2x+15=2(x+1)+11...
kerimok607
kerimok607
05.09.2020 20:52
Самолёт летит со скорость 864 км/ч. сколько метров он преодолевает за одну секунду?​...
ленаискакова
ленаискакова
30.10.2021 12:08
Каптал в 10 000 поделите на 3 части так, что бы первая часть была на 2000 больше второй и на 3000 больше - третьей. В ответ запишите чему будет равна вторая часть. ​...
uliana20003
uliana20003
21.05.2020 12:55
Ребята купили коробку леденцов, стали раздавать по 3 леденца, всё было хорошо, но последнему человеку леденцов совсем не досталось. Тогда поделили леденцы заново: раздали...
00Алекс00
00Алекс00
28.05.2022 06:57
Найдите : sinα, tgα, ctgα, если cosα= - 5/13 π/2 α π...
invisiblefibers
invisiblefibers
13.06.2022 07:55
B 2аya2 +ba+ формуласынқолданып, V51 санының мәнінесепте. Жауабын 0,01-ге дейінгідәлдікпен, кемімен алынғанжуықтаумен жаз.Жауабы онлайн мектеп ответ ответ...
kolyakuzmin2006
kolyakuzmin2006
03.08.2022 13:47
Найти значение: (-1 2/3+1,6): (-0,2) и результат возвести в квадрат....
hoteleleon3
hoteleleon3
03.08.2022 13:47
Сколько корней имеет уравнение x=4+√x+38 1)два 2)один 3)нет корней 4)три...
anaumova21
anaumova21
29.05.2021 02:23
Найдите значение выражения z^3 - 64/z^3,если z-4/z= -2...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку
О НАС
СООБЩЕСТВО
ПОМОЩЬ
App
.
.
logo
Начни делиться знаниями
Вход Регистрация
Что ты хочешь узнать?
Спроси ai-бота