Пусть - координаты точки касания касательной.
Производная данной функции:
Поскольку касательная параллельна прямой y = 3x + 7, то у них угловые коэффициенты равны, а тогда по геометрическому смыслу производной, мы получим
Тогда ордината
ответ: 1.
Пусть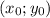 - координаты точки касания касательной.
- координаты точки касания касательной.
Производная данной функции: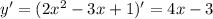
Поскольку касательная параллельна прямой y = 3x + 7, то у них угловые коэффициенты равны, а тогда по геометрическому смыслу производной, мы получим
Тогда ордината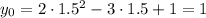
ответ: 1.