Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
вероника03
22.07.2022 19:38 •
Алгебра
Вычислить предел функции, не используя правило Лопиталя. lim x стремится к бесконечности (3x - 1 / 3x + 2)^6x+1 = ?
Показать ответ
Ответ:
Sverona
16.05.2021 18:10
(см. объяснение)
Объяснение:
Условие:
Замена:
.
Итого получили, что ответ:
Задание выполнено!
0,0
(0 оценок)
Популярные вопросы: Алгебра
moȗnuk
30.08.2020 13:02
Прямоугольный участок земли обнесён забором,длина которого 40 м.площадь участка равна 96 м^2.найдите длины сторон участка....
londi17
06.03.2020 01:15
Уменя в этом примере не сходится ответ,.заранее ! 1)вычислить: a) (17,2 * 4.01 + 4.01 * 32.8) : 1 2/3 б) 1/2 - * 2 2/3 - 25 * 0.03 * 4...
ира1288
06.03.2020 01:15
Корень из 6*40 умножить на корень из 90...
Dalishka808
06.03.2020 01:15
Подскажите как складывать и вычитать корни? пример: корень из 19 + корень из 7...
esmirakagraman
11.02.2020 15:44
2*0,6*(-0,8) это сколько получается...
vkuke
11.02.2020 15:44
Люди, ! вычислите значение tga, если sina=3/5 и пи/2...
lusy43p08hli
27.03.2023 12:06
1)sin 2t/t-sin t 2) sint/(2cos(t/2)) 3) cos квадрат(x+пи на 3)=1 уравнение...
DEN23567893
27.03.2023 12:06
Скорость автомобиля90 км/ч. какое расстояние он проезжает за один час?...
Qwerty23459484
27.03.2023 12:06
Как решить уравнение 6(х-12) больше равно 3(х-4...
диёра2010
07.12.2020 19:19
Найдите значение выражение корень 10а+11b,ели a =39,b=-6...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
(см. объяснение)
Объяснение:
Условие:
Замена: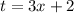 .
.
Итого получили, что ответ:
Задание выполнено!